Ấn Độ, cái nôi của hệ đếm hiện đại

Georges IFRAH

Phải trao cho dân tộc nào vinh dự đã phát minh hệ đếm hiện đại này, quan trọng chẳng khác gì khám phá lửa, bánh xe tròn hay máy chạy bằng động cơ hơi nước? 

Vào đầu thế kỷ XX, một số nhà viết sử khẳng định rằng chúng ta có hệ đếm là nhờ các nhà toán học Hy Lạp cổ. 

Theo họ, hệ đếm viết hiện nay đã nảy sinh ở Hy Lạp vào đầu CN. Từ hải cảng Alexandrie, hệ được truyền sang La Mã vào thời đế chế và sau đó, nhờ giao thương mà tới được Trung Đông và Ấn Độ. Từ La Mã, hệ được lan truyền đến Tây Ban Nha và các tỉnh Bắc Phi, nơi người A Rập phương Tây lúc bấy giờ đã tìm thấy nó trong các cuộc chiến chinh của họ. Và từ đó, hình thành, một bên là dạng hoạ hình chữ số Ấn Độ và A Rập phương Đông, và một bên rõ ràng khác biệt, đó là dạng hoạ hình chữ số Maghreb và châu Âu. 

Giải thích hấp dẫn, nhưng không dựa trên một cơ sở lịch sử nào, vì đến ngày nay không có một dấu vết gì chứng tỏ người Hy Lạp thời cổ đã sử dụng một hệ tương tự. 

Lý thuyết này hẳn là dựa vào những xác nhận không bằng chứng mà trước hết chỉ nhằm tán dương cái gọi là “phép lạ Hy Lạp”. 

Thực ra là trong suốt thời Thượng cổ, người Hy Lạp chỉ dùng hai loại ký hiệu số. Loại thứ nhất, tương đương về mặt toán học với ký hiệu số của người La Mã, và loại thứ hai thuộc dạng Alphabet như của người Do Thái. Nhưng cả hai ký hiệu không cái nào dựa vào nguyên tắc vị trí định lượng và đều không có con Zéro. 

Vả lại, các thiên tài toán học Hy Lạp rõ ràng không thể không cảm nhận được giá trị của hai phát minh này: lẽ ra là họ có thể thừa nhận chúng nếu chúng đã được sinh ra trên đất nước họ hay dù họ chỉ nghe nói tới chúng mà thôi. 

Người Hy Lạp đã để lại cho chúng ta không nhiều tài liệu về các kỹ thuật thao tác của họ. Nhưng người ta biết là họ đã làm được những bài tính rất phức tạp. Trong một cuốn chuyên luận nhỏ tựa đề là Arénaire (“sống trong cát” – ND), nhà bác học Archimède (khoảng 287-212 trước CN) đã tính số lượng hạt cát chứa trong “quả cầu vũ trụ” (quả cầu có đường kính bằng khoảng cách từ Trái đất đến các ngôi sao cố định). Và ông đã tìm thấy một con số xấp xỉ con số có thể được biểu hiện trong hệ hiện nay, bằng con số “1” tiếp theo là sáu mươi bốn Zéro! 

Nhưng các bài tính này nói chung không phải thực hiện nhờ có chữ số, vì cả hai hệ đếm Hy Lạp đều không sử dụng được trong các phép tính số học. Người Hy Lạp, như ta đã thấy, chỉ làm tính với hòn sỏi hay thẻ tròn trên bàn tính, loại bàn trên đó có kẻ sẵn từng cột phân chia các cấp thập phân. Tuy nhiên, đáng lẽ ngay quan niệm về dụng cụ làm tính này rất có thể gợi hứng trước tiên cho các nhà số học Hy Lạp để khám phá ra nguyên tắc vị trí định lượng, và sau đó con Zéro để rồi cho ra hệ đếm sử dụng được. Nhưng họ đã không làm điều đó vì không quan tâm tới khía cạnh thực dụng. 

Kỳ thực, nếu chúng ta có được một hệ đếm đơn giản hoá là nhờ những thế hệ bác học và các nhà làm tính, trái với người Hy Lạp, đã có khuynh hướng đi sâu vào các ứng dụng thực tế và được khích động bởi lòng say mê phép tính và các con số lớn. 

Thật vậy, ở miền Bắc Ấn Độ, vào khoảng thế kỷ V sau CN, tổ tiên của hệ đếm hiện đại đã chào đời và đã thiết lập những nguyên tắc cơ bản của phép tính viết như chúng ta thực hành ngày nay. 

Nhiều tư liệu và bằng chứng và ngay chính người A Rập (vốn được gán nhầm là đã phát minh ra hệ đếm này) cũng luôn khẳng định điều đó. 

Nhưng quá trình này còn đoi hỏi rất nhiều thời gian và khối óc giàu tưởng tượng! 

Hệ đếm cổ Ấn Độ: ngõ cụt 

Trước khi đạt đến hệ đếm trên, nhiều ghi chép vào thời kỳ từ thế kỷ III trước CN - thế kỷ VII sau CN cho thấy người phương Bắc Ấn Độ đã sử dụng rất lâu một hệ đếm viết tuy rất thô sơ nhưng cũng có một trong những đặc tính của hệ đếm hiện đại. 

Chín chữ số đầu tiên của hệ này (chữ số của đơn vị đơn) quả nhiên là những ký hiệu tách rời khỏi mọi trực giác nhạy bén: tất cả đều khác hẳn nhau và không nhằm gợi lên cho thị giác những số lượng tương ứng nữa. Ví dụ số 9, không còn được tạo nên bởi chín gạch hay chín điểm; nó chỉ tương ứng với một nét chữ quy ước:

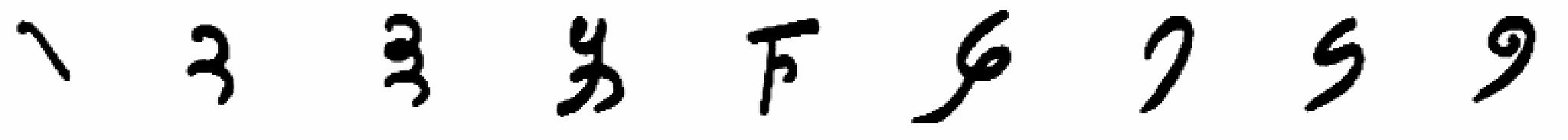
(1 2 3 4 5 6 7 8 9)

Hơn nữa, chúng đã báo hiệu trước chín chữ số có ý nghĩa hiện nay: vài thế kỷ sau, chính là từ những ký hiệu này đã nảy sinh ra chữ số mà tới bây giờ chúng ta vẫn gọi nhầm là “chữ số A Rập”.

Nhưng vì không theo nguyên tắc vị trí định lượng, nên chữ số này chưa vận hành được như chữ số ngày nay. Từ cơ số mười, hệ đếm này dựa trên nguyên tắc cộng vào và gán một chữ số đặc biệt cho mỗi số:

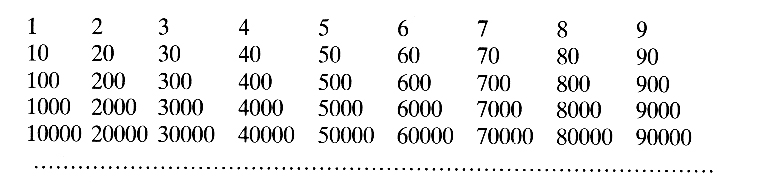
Vậy nó gồm những chữ số riêng biệt, không chỉ cho mỗi đơn vị đơn, mà còn cho hàng chục, hàng trăm, hàng nghìn và hàng chục nghìn. Và để thể hiện một con số như 7629, phải sắp cạnh nhau, trong thứ tự này, những chữ số “7 000”, “600”, “20”, “9”:

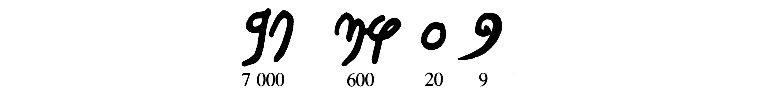
Tương tự như một số hệ đếm thời cổ, hệ đếm này rất giới hạn. Các phép tính số học, dù chỉ là phép cộng đơn giản, đều không thể được.

Chi tiết của một văn khắc Phật giáo trên vách động Nānā Ghā (thế kỷ II trước CN). Chỗ tô đậm: thể hiện số 24 400 (chữ số 20 000, 4 000 và 400 nối tiếp nhau từ trái sang phải). Hơn nữa, chữ số lớn nhất tương ứng với 90 000, và không có chuyện vượt qua 99 999! Hệ đếm cổ lỗ này không thể nào thoả mãn nhu cầu của các nhà bác học Ấn Độ, đặc biệt các nhà thiên văn, những người, ngay từ thời cổ xưa, đã ham thích những con số lớn.

Thay vì các chữ số, một ký hiệu viết cả chữ

Nhưng đã từ lâu, họ biết khắc phục khó khăn bằng cách mượn tên số trong tiếng Phạn (ngôn ngữ bác học Ấn Độ xưa nay vẫn là công cụ liên kết giữa các nhà thông thái và bác học không cùng ngôn ngữ). Vì không thể biểu hiện những con số lớn bằng chữ số, họ sớm nghĩ ra cách diễn tả chúng bằng “cả chữ”. Họ đã vô tình dấn thân vào con đường khám phá nguyên tắc vị trí định lượng và con Zéro bởi lẽ hệ này đã mang mầm mống của hai khám phá cơ bản này. Hệ đếm miệng này quả thực tuyệt vời. Trước tiên họ cho mỗi số trong chín số nguyên đầu tiên một tên riêng:

eka dvi tri catur paňca sat sapta asta nava
(1 2 3 4 5 6 7 8 9)

Xây dựng trên cơ số mười, tiếp đó hệ này gán một tên riêng biệt cho hàng chục và mỗi lũy thừa của nó, rồi tên ghép cho tất cả số khác.

Nhưng thay vì tiến hành như chúng ta theo lũy thừa mười thoái, kể từ khoảng thế kỷ IV sau CN, các nhà bác học Ấn Độ có thói quen biểu hiện các số theo thứ tự lũy thừa tiến của cơ số, khởi đầu bằng các đơn vị đơn tương ứng. Và thay vì đọc “ba nghìn bảy trăm chín”, các nhà toán học và thiên văn Ấn Độ lại diễn tả bằng tiếng Phạn như sau:

nava sapta sata ca tri sahasra 
«chín, bảy trăm và ba nghìn»

Hơn nữa, ngược lại với hệ đếm miệng hiện đại (ví dụ những số 10 000, 100 000, 10 000 000, 100 000 000 được gọi “mười nghìn”, “trăm nghìn”, “mười triệu” và “một trăm triệu”, với tên của nghìn, của triệu giữ vai trò cơ số phụ), hệ đếm miệng của các nhà bác học Ấn Độ không ưu đãi một con số nào cả. Họ dành cho các lũy thừa mười những tên hoàn toàn độc lập với nhau:

10                         dasa
100                       sata
1000                     sahasra
10000                   ayuta
100000                 laksa
1000000               prayuta
10000000             koti
100000000           vyarbuda
1000000000         padma 

....................        ...............

Để biểu hiện một con số nào đó, thì chỉ cần đặt tên chỉ hàng chục (dasa) giữa tên các đơn vị đơn và tên đơn vị thuộc cấp 2, tên chỉ hàng trăm (sata) giữa tên các đơn vị đơn thuộc cấp 2 và 3, rồi tên của hàng nghìn (sahasra) giữa tên các đơn vị đơn thuộc cấp 3 và 4, và cứ như thế, thuận theo chiều hướng đọc như trên.

Cho nên, một con số lớn như:

(“bốn trăm bốn mươi sáu triệu tỷ, bảy trăm bốn mươi hai triệu triệu, một trăm bảy mươi ba tỷ, bảy trăm hai mươi chín triệu, năm trăm năm mươi mốt nghìn sáu trăm ba mươi sáu”) 

được các nhà toán học Ấn Độ xướng lên một cách vắn tắt hơn và rõ ràng hơn chúng ta nhiều:

6, 3 dasa, 6 sata, 1 sahasra, 5 ayuta, 5 laksa, 9 prayuda, 2 koti, 7 vyarbuda, 3 padma, 7 kharva, 1 nikharva, 2 mahapadma, 4 sankha, 7 samdra, 6 madhya, 4 antya, 4 pararddha.

(Dịch từng chữ : «SÁU, BA chục, SÁU trăm, MỘT nghìn …»)

Nhưng thế vẫn chưa đủ. Còn cần những tiến bộ mới.

Thiên tài sáng tạo của các nhà bác học Ấn Độ

Cách xem xét lũy thừa mười theo thứ tự đều đặn và dãy liên tiếp bất biến đã đem đến một sự chuyển biến vĩ đại vào thế kỷ V sau CN.

Vì muốn rút gọn, các nhà toán học và thiên văn Ấn Độ đương thời đã vượt qua một giai đoạn quan trọng: họ bỏ đi, trong thân của biểu hiện số, tất cả tên chỉ cơ số và chỉ các lũy thừa (dasa “mười”, sata “trăm”, sahasra “nghìn”, v.v.). Từ nay, trong cách đọc số, họ chỉ giữ lại dãy liên tiếp các tên đơn vị tương ứng đồng thời tôn trọng thứ tự chuỗi đều đặn và phù hợp với cách đọc theo lũy thừa tiến thập phân.

Từ đó, một con số như 7 629 được biểu hiện như sau:

“CHÍN. HAI. SÁU. BẢY” (=9 + 2 x 10 + 6 x 100 + 7 x 1 000)

Trong quá trình đơn giản hoá này, các nhà bác học Ấn Độ đã nghĩ ra một hệ đếm miệng dùng vị trí định lượng thật sự, các tên bằng tiếng Phạn của chín đơn vị đơn nhận một giá trị biến thiên tuỳ theo vị trí của nó trong phát biểu số. Ví dụ khi đọc: “MỘT, MỘT”, người ta dành một giá trị đơn cho cái Một đầu tiên và một giá trị hàng chục cho cái thứ hai. Còn ấn tượng hơn nữa khi biết các nhà bác học Ấn Độ là những người duy nhất đã phát minh ra một cách đếm miệng hoàn toàn dựa trên quy tắc này. Nhưng tiến bộ này sẽ sớm buộc có một tiến bộ khác, cũng không kém cơ bản.

Hãy lấy hai ví dụ đơn giản. Trong hệ đếm này, một số như 321 được biểu hiện khá dễ dàng bằng cách đọc:

“MỘT. HAI. BA” (= 1 + 2 x 10 + 3 x 100)

Ngược lại, khó mà biểu lộ một số như 301, trong đó thiếu hàng chục. Người ta không thể đành lòng đọc:

“MỘT. BA”

bởi vì có nghĩa là ba mươi mốt, mà không là ba trăm lẻ một: chúng ta cần có một chữ riêng biệt để báo cho biết ở đây không có hàng chục.

Khi người ta áp dụng chặt chẽ nguyên tắc vị trí định lượng cho các tên của chín đơn vị đơn, việc sử dụng một từ ngữ đặc biệt là tuyệt đối bức thiết để đánh dấu những đơn vị vắng mặt thuộc một hàng nào đó.

Các nhà bác học Ấn Độ đã khắc phục khó khăn bằng cách dùng từ śūnya có nghĩa là “rỗng”. Và con số 301 được phát biểu như sau:

eka śūnya tri
«MỘT.RỖNG. BA»

Mọi điều lập lờ từ nay bị loại bỏ. Sau người Babylone và chắc là cùng thời với người Maya, người Ấn Độ cũng vừa phát minh ra con Zéro. Như vậy, các nhà bác học Ấn Độ có sẵn trong tay mọi nguyên liệu cần thiết để xây dựng một hệ đếm hiện đại:

- để chỉ đơn vị từ 1 đến 9, họ dùng những chữ số khác nhau và tách hẳn với mọi trực cảm thị giác;

- họ đã biết nguyên tắc vị trí định lượng;

- và họ vừa mới khám phá con Zéro.

Tuy nhiên ở giai đoạn này, vấn đề vẫn chưa chín muồi. Chín chữ số còn chưa theo nguyên tắc vị trí định lượng vì lúc đó quy tắc này chỉ áp dụng cho các tên số tiếng Phạn. Còn về số Zéro, nó chỉ mới được biểu thị bằng lời.

Chính là sự kết hợp của ba ý tưởng lớn nói trên đã tạo ra phép lạ.

Cả hai khám phá quy tắc vị trí định lượng và con Zéro có trễ nhất là từ thế kỷ V sau CN.

Người ta tìm thấy những ví dụ đầu tiên trong một cuốn sách vũ trụ luận, mang tên Lokavibhāga, do các thành viên của một phong trào tôn giáo Ấn Độ có tên jaïni xuất bản ngày 25 tháng Tám năm 458 theo lịch Julien. (Người ta có thể chắc chắn về ngày tháng này, bởi vì chúng được chỉ định rõ ràng trong văn bản bằng ngày tháng tương đương trong một kỷ nguyên Ấn Độ được dùng thời bấy giờ; hơn nữa, chúng được xác nhận bằng những ghi chú liên quan đến một số dữ kiện thiên văn đã được biết đến và ngày nay được ghi ngày tháng.)

Trong văn bản này, ví dụ con số 14 236 713 được biểu hiện như sau:

trīny ekam sapta sat trīni dve catvāry ekakam

(Dịch từng từ: 

“BA. MỘT. BẢY. SÁU. BA. HAI. BốN. MỘT”)

Còn các số như 13 107 200 000, có những đơn vị thiếu, được biểu hiện một c ách không thể nhầm lẫn nhờ từ śūnya:

Śūnya śūnya śūnya śūnya śūnya dvi sapta śūnya eka tri eka
(“Rỗng. Rỗng. Rỗng. Rỗng. Rỗng. Hai. Bảy. Rỗng. Một. Ba. Một”)

Đáng chú ý là mỗi lời đếm được xác định trong văn bản bằng tiếng Phạn:

sthānakramād 
(từng từ một: “trong thứ tự vị trí”)

Các tác giả của chuyên luận, đã muốn gửi tác phẩm của họ đến đối tượng có thể gọi là một “quần chúng rộng rãi”. Bởi lẽ ngoài những giải thích rõ ràng về cách thể hiện này, họ hoàn toàn tránh các chi tiết quá kỹ thuật và sử dụng các thuật ngữ quá chuyên môn đối với những người bình thường và trước hết, họ muốn khoe trương công trạng của khoa học và phong trào tôn giáo của họ. 

Cách đếm này đã được biết đến rộng rãi ở Ấn Độ vào giữa thế kỷ V và hẳn là đã được lan truyền ra ngoài giới bác học. 

Từ đó, hệ đếm này đã đạt được thành công đáng kể trong giới các nhà toán học và thiên văn Ấn Độ và được đã số sử dụng cho đến hồi gần đây. 

Từ thế kỷ VI, hệ này được lan truyền ra ngoài biên giới Ấn Độ: các thợ khắc văn tự trên đá của các nền văn minh Khmer (Campuchia), Chàm (vùng Đông Nam Việt Nam), Java v.v., sử dụng rộng rãi để biểu hiện ngày tháng của họ. Điều này không có gì đáng ngạc nhiên, vì ngay những thế kỷ đầu Công nguyên, các nền văn hoá Đông Dương và Indonesia xưa đã chịu ảnh hưởng rất mạnh từ Ấn Độ, một phần, vì bành trướng của đạo Shiva và đạo Phật, và phần khác, vì vai trò môi giới quan trọng của những xứ này trong việc buôn bán gia vị, tơ lụa và ngà voi giữa Ấn Độ và Trung Hoa…

(Trích đoạn Chương 9, sách Chữ số hay Lịch sử một phát minh vĩ đại)