Sur la matière - II

- Nguyễn Quang — published 10/12/2013 19:35, cập nhật lần cuối 12/04/2016 22:21

Tout ce que vous avez toujours
voulu savoir sur la matière sans
oser le demander – Part-II

Nguyễn Quang

3-De Maxwell à Einstein

Le second nuage qui obscurcissait le ciel de Lord Kelvin, c’était l’expérience de Michelson-Morley de 1887, qui tendait à infirmer l’hypothèse de l’éther et, du coup, à confirmer la persistance d’une contradiction fondamentale entre la mécanique rationnelle de Newton et la théorie électromagnétique de Maxwell. Il est temps de visiter ce troisième monument de la physique du 19^ème siècle, synthèse majestueuse de l’électricité et du magnétisme, mais aussi de l’optique.

En passant sur la préhistoire de cette science, on peut dire que l’optique – comment la lumière voyage-t-elle, sous quelle forme, suivant quelles lois ? – débute au 17^ème siècle avec les études de Descartes sur les couleurs et la réfraction, mais surtout avec les théories antagonistes de Newton et Huygens sur la nature de la lumière. Fidèle à son approche mécaniste, Newton promeut une conception corpusculaire qui lui permet, à partir du mouvement de «grains de lumière» assimilés à des points matériels, d’expliquer naturellement les phénomènes de dispersion, plus difficilement de réfraction, mais pas du tout d’interférence ou de diffraction. De son côté, la théorie ondulatoire de Huygens, où la lumière se propage dans un milieu hypothétique baptisé éther, à la manière des ondes dans l’eau, explique naturellement les interférences, mais il faudra attendre les contributions, au début du 19^ème siècle, de Young et Fresnel sur la diffraction et la polarisation, pour qu’elle l’emporte sur celle de Newton.

La synthèse ondulatoire

Enfin, en 1854 puis 1864, la grande synthèse opérée par Maxwell va permettre de réunir les phénomènes électriques, magnétiques et optiques sous l’égide d’un même concept, le champ électromagnétique. La notion de champ en physique a été introduite dans les années 1830 par Faraday, dans ses études expérimentales sur l’induction. La définition mathématique est on ne peut plus simple : la donnée d’un champ dans l’espace ou dans l’espace-temps, c’est la donnée en tout point (repéré par un vecteur de position r dans l’espace, par un couple (r,t) dans l’espace-temps) d’une ou plusieurs fonctions Φ(r) ou Φ(r,t) qui dépendent continûment de ce point. Ainsi, en physique classique, le champ vectoriel électrique E(r) ou le champ vectoriel magnétique B(r), qu’on peut visualiser expérimentalement avec de la limaille de fer qui s’oriente le long des «lignes de force» du champ (voir fig.3.1). Maxwell s’appuie sur les travaux de ses prédécesseurs Gauss, Ampère et Faraday, mais, comme le soulignent Einstein et Infeld (cités dans [CTS]), la notion de champ électromagnétique qu’il introduit dans sa théorie est une innovation conceptuelle majeure par rapport à la mécanique rationnelle : «Les équations de Maxwell décrivent la structure du champ électromagnétique. Tout l’espace est la scène de ces lois et non pas, comme pour les lois mécaniques, les points seulement où de la matière et des charges sont présentes (…) Le champ ici et maintenant dépend du champ immédiatement voisin à un instant immédiatement antérieur. Les équations nous permettent de prévoir ce qui se passera un peu plus loin dans l’espace et un peu plus tard dans le temps, si nous connaissons ce qui se passe ici et maintenant (…) Le résultat d’une telle déduction est l’onde électromagnétique.» (fig. 3.2). L’existence de telles ondes fut établie expérimentalement en 1888 par Hertz (d’où le nom «d’ondes hertziennes»).

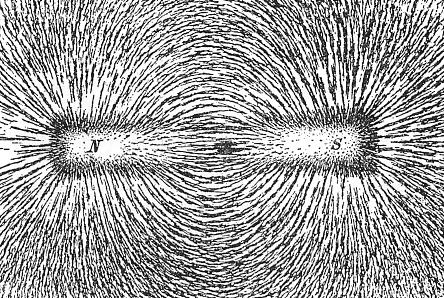
hinh31

Fig. 3.1 Visualisation d’un champ magnétique

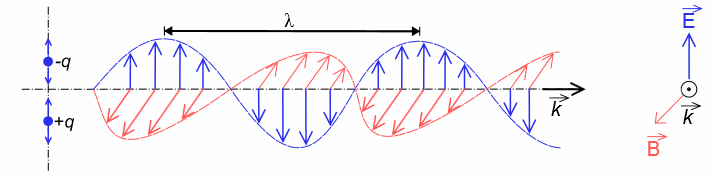
hinh32

Fig. 3.2 Schématisation d’une onde électromagnétique. λ : longueur d'onde;
E: Champ électrique oscillant; B: Champ magnétique oscillant

De fait, les quatre équations vectorielles aux dérivées partielles obtenues par Maxwell en 1854 prédisaient l’existence d’une onde associée aux oscillations des champs électrique et magnétique et se déplaçant dans le vide à une vitesse facilement accessible par l’expérience. La concordance de cette vitesse (aux incertitudes expérimentales près) avec la vitesse de la lumière amena Maxwell à conclure en 1864 «que la lumière et l’électromagnétisme sont deux phénomènes de même nature et que la lumière est une perturbation électromagnétique se propageant dans l’espace suivant les lois de l’électromagnétisme ». La synthèse des phénomènes ondulatoires était ainsi réalisée.

$div\vec{D}=\rho$    (1)
$div\vec{B}=0$    (2)
$\vec{rot}\vec{E}=\,- \frac{\partial \vec{B}}{\partial t}$    (3)
$\vec{rot}\vec{H}=\vec{j}+ \frac{\partial \vec{D}}{\partial t}$ (4)

Mais dans le même temps une synthèse éventuelle avec la mécanique s’éloignait. On ne parle pas ici de la dualité onde-corpuscule (voir section 4), mais d’incompatibilités plus fondamentales :

Les équations de Maxwell ne sont pas invariantes dans un changement de repères galiléens ( i.e. un changement entre deux référentiels inertiels en mouvement relatif rectiligne et uniforme), autrement dit elles sont en conflit avec le principe de relativité galiléen selon lequel «deux référentiels galiléens sont équivalents pour les lois de la mécanique» ; elles impliquent que la vitesse de la lumière dans le vide, notée usuellement c, est indépendante des repères galiléens alors que, suivant les lois de la cinématique classique, elle devrait se composer avec leur vitesse relative.

L’idée répandue à l’époque étant que des ondes ne peuvent pas se propager sans support, le vide était assimilé à l’éther, un substrat hypothétique censé porter la lumière, doté de propriétés contradictoires – suffisamment «rigide» pour transporter de l’énergie, suffisamment «fluide» pour ne pas entraver le mouvement des corps matériels, mais suffisamment «présent» pour induire des effets observables. Sous-entendant que tout mouvement devait être considéré relativement à un éther fixe (et donc fournissant un référentiel absolu), on cherchait par exemple à mettre en évidence un «vent d’éther» dû au mouvement de la Terre. Or, en 1887, l’expérience de Michelson et Morley, probablement «l’expérience négative» la plus célèbre de l’histoire de la science, obligea à conclure à l’inexistence de ce vent d’éther, car des mesures interférométriques extrêmement précises n’avaient pas pu mettre en évidence la moindre variation de c suivant le déplacement de la Terre. Partout qu’on se tournât, on trouvait des contradictions.

La révolution relativiste

Entre 1892 et 1904,Hendrik Lorentz établit par tâtonnements des transformations de coordonnées laissant invariantes les lois de Maxwell. Poincaré montra qu’elles formaient un groupe (au sens mathématique, voir section 6 [à venir] ), baptisé groupe de Lorentz, et à partir duquel il déduisit pratiquement toutes les équations de ce qu’on appelle aujourd’hui la théorie de la relativité restreinte («Sur la dynamique de l’électron», 1905). C’est toutefois à Einstein («Sur l’électrodynamique des corps en mouvement», 1905) que les historiens des sciences attribuent généralement la paternité de la relativité, à cause de l’interprétation physique – révolutionnaire – qu’il en donne.

L’impasse des années 1900 provenait du conflit entre les lois de Maxwell, qui impliquaient l’invariance de c, et les lois de la cinématique classique, qui commandaient que les vitesses se composent. Or les premières pouvaient se targuer de multiples confirmations expérimentales, alors que les secondes reposaient uniquement sur le postulat de l’indépendance mutuelle d’un temps et d’un espace absolus. Avec une audace intellectuelle égale à celle de Planck avant lui, Einstein opte pour Maxwell et fonde sa théorie sur deux principes : il conserve le principe de relativité galiléen en l’étendant à tous les événements physiques ; il lui adjoint l’invariance de c dans tous les référentiels galiléens. Il retrouve par des arguments physiques les transformations de Lorentz, qui deviennent ainsi les transformations naturelles entre référentiels galiléens.

Dans un mouvement où seule varie la première coordonnée spatiale (on peut toujours s’y ramener), elle s’écrivent :

c∆t' = γ(c∆t – β∆x)

∆x' = γ(∆x – βc∆t)

∆y' = ∆y

∆z' = ∆z

$$ \Delta t' = \frac{\Delta t - v\Delta x/c^2}{\sqrt{1-v^2/c^2}}$$ $$ \Delta x'= \frac{\Delta x - v\Delta t}{\sqrt{1-v^2/c^2}} $$

∆y' = ∆y

∆z' = ∆z.

En posant $ \beta =\frac{v}{c}$ et $ \gamma = \frac{1}{\sqrt{1-\beta^2}} $

Sous forme matricielle :

$ \begin{bmatrix} c\Delta t' \\ \Delta x' \\ \Delta y' \\ \Delta z' \end{bmatrix} = \begin{bmatrix} \gamma & - \beta\gamma & 0 & 0\\ - \beta\gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} c\Delta t \\ \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} $

On constate que non seulement ces formules redonnent approximativement la cinématique galiléenne à des vitesses non relativistes (i.e. négligeables par rapport à c), mais qu’elles impliquent aussi que la vitesse de la lumière est une limite indépassable. Partant de l’impossibilité de transmission d’information instantanée à distance, Einstein remet hardiment en cause le caractère absolu du temps lui-même. Le nouveau paradigme devient un continuum quadridimensionnel que Minkowski baptisera en 1908 espace-temps, sur lequel le groupe de Lorentz agit en conservant simplement «l’intervalle d’univers» (ou pseudo-norme).

Δs² = c²Δt²– Δx² – Δy² – Δz² = c²Δt² – Δl²

Pour passer de la cinématique à la dynamique relativiste, il faut remplacer les grandeurs vectorielles habituelles, vitesse et quantité de mouvement, par le quadrivecteur vitesse (où tau est le temps propre de la particule)

$ \mathbf{u} = \left( c\frac{dt} {d\tau}, \frac{dx} {d\tau}, \frac{dy} {d\tau}, \frac{dz} {d\tau} \right), $

et le quadrivecteur énergie-impulsion (où E est l’énergie et m la masse)

P = mu = (E/c, p_x, p_y, p_z) ; avec :

$E/c = mc\frac{dt} {d\tau}$; $p_x = m\frac{dx} {d\tau}$ ; $p_y=m\frac{dy} {d\tau}$ ; $ p_z=m\frac{dz} {d\tau} $ ,

Comme ce quadrivecteur est proportionnel à la quadrivitesse (qui est de pseudo-norme c) par des coefficients invariants par changement de référentiel inertiels, on a, dans tout référentiel inertiel :

$(E/c)^2 - (\vec{p}\,)^2 = m^2.c^2 $

C’est la «relation de dispersion» fondamentale de la mécanique relativiste, où l’on peut vérifier que la premier membre est invariant par le groupe de Lorentz, et donc la masse m donnée par m² = (E² – p²c²)/c⁴, appelée masse invariante, est indépendante de tout référentiel galiléen. En particulier, dans un référentiel où la particule est immobile, sa masse invariante est égale à sa masse au repos et l’équation devient la formule universellement connue E₀ = m.c², qui signifie que, même au repos, un corps matériel renferme une certaine énergie, qui peut être énorme à cause de la valeur élevée de c. Dans le même référentiel, si la particule de masse non nulle m se meut à une vitesse v, son énergie est donnée par la formule $$E = \gamma.mc^2 = \frac{mc^2}{\sqrt{1-(v^2/c^2)}},$$ (où γ est le facteur relativiste et γ.m est parfois appelée la masse en mouvement, mais c’est une source de confusion, de même d’ailleurs que la masse au repos). Notons encore une fois qu’aux vitesses non relativistes, nous obtenons une approximation des résultats classiques, ici de l’énergie cinétique additionnée à l’énergie au repos. Quand la vitesse v augmente pour tendre vers c, le dénominateur du facteur relativiste tend vers zéro et donc, pour une particule de masse non nulle donnée, l’énergie E tend vers l’infini, mais comme il ne peut pas y avoir d’énergie infinie, cela signifie simplement qu’il est impossible d’accélérer indéfiniment une particule lorsque sa vitesse approche de c. A l’inverse, si une particule (comme le photon) se déplace à la vitesse de la lumière, c’est qu’elle a nécessairement une masse nulle. On retrouve ainsi une des questions qu’on s’était posées au départ : comment une particule peut-elle être de masse nulle ?

Il paraît ici indispensable de revenir sur les problèmes épistémologiques posés par les notions de masse et de force dans la mécanique rationnelle classique. Dans ses Principia, Newton nous avertit qu’il utilise le langage intuitif commun pour définir la masse d’un corps comme étant la quantité de substance, de matière contenue dans ce corps. Quant à la nature de cette matière, il se réfugie derrière sa formule célèbre, «hypotheses non fingo», «je ne fais pas d’hypothèses». Mais dans ses quatre lois fondamentales (en fait, des principes), il glisse ensuite deux définitions a priori différentes de la masse : dans la seconde loi, la masse inertielle est définie par la relation fameuse force = masse * accélération, c-à-d. que la masse inertielle d’un corps est ce qui s’oppose à sa mise en mouvement ; puis dans la troisième loi, la masse gravitationnelle est définie par la loi d’attraction universelle entre deux corps.

L’égalité entre ces deux masses est certes vérifiée expérimentalement à 10^-12 près, et l’on peut la présenter comme un «principe d’identité». Mais ce qui fait débat, c’est la notion de force, facile à saisir intuitivement mais difficile à appréhender conceptuellement. On peut se rendre compte rapidement du caractère circulaire des définitions posées par Newton (comme d’ailleurs de toutes les définitions dans tous les dictionnaires) et se retrouver, comme Poincaré, «acculé à la définition suivante, qui n’est qu’un aveu d’impuissance : les masses sont des coefficients qu’il est commode d’introduire dans les calculs». Mais on voit bien que ces calculs conduisent à des résultats et prédictions corrects dans un cadre déterminé, en ce sens que, dans ce cadre, ils sont validés par l’expérience. Et par les applications techniques⁽¹⁾. Par exemple, dans le cadre relativiste, les si contre-intuitives contractions de l’espace et du temps prédites par les formules de Lorentz, l’homme de la rue s’en sert tous les jours à travers son système GPS. On ne voit alors aucun inconvénient à adopter le point de vue «empiriste» résumé dans l’injonction de Dirac (ou de Feynman, l’histoire est probablement apocryphe) : «Shut up and calculate!» Après tout, nul besoin de voir des photos d’atomes (section 1) pour adhérer à une théorie atomiste qui nous donne depuis des décennies les preuves de sa (même trop) grande efficacité: la bombe A, les centrales nucléaires, toutes les applications quotidiennes des théories relativistes. Pour les théories quantiques, voir la section 4.

L’équivalence masse-énergie révélée par l’équation d’Einstein permet de répondre à un certain nombre de questions qu’on se posait dans la section précédente sur les atomes et les particules :

*Indépendamment de toute référence à un grain de matière ou un corpuscule matériel, le mot particule désignera un quantum d’énergie, qui pourra se présenter sous forme d’énergie (ce sera une particule-énergie ou une particule sans masse) ou sous forme massique (ce sera une particule matérielle). Mais l’équivalence d’Einstein n’est pas une identité, sinon la matière et l’énergie se transformeraient anarchiquement l’une en l’autre, ce qui n’est pas le cas. «Rien ne se perd, rien ne se crée, tout se transforme», disait Lavoisier à la suite de Lucrèce. Ce sont justement les règles de transformation énergie/matière que les théories quantiques vont tenter de cerner.

*Sans pouvoir expliquer en détail la «force de liaison» au sein des noyaux atomiques, l’équivalence d’Einstein permet au moins d’en comprendre les manifestations. Ainsi une particule alpha, c-à-d. un noyau d’hélium, est moins massive d’environ 1% que l’ensemble des 2 protons et 2 neutrons qui la composent. Inexplicable par la physique classique, ce «défaut de masse» représente l’énergie de liaison, soit environ 28 MeV. Plus spectaculaire encore est la fission nucléaire, quand un noyau lourd capte une autre particule et le noyau composé se désintègre en plusieurs fragments. Dans l’exemple d’un noyau de masse M qui fissionne en deux autres noyaux de masses m et m’ , la relation de dispersion relativiste permet de montrer facilement que M >m+m’ et de calculer le défaut de masse M – (m+m’). A l’échelle humaine, la multiplication par le facteur c² produit une énergie sans commune mesure avec celle des réactions chimiques. Ainsi, dans la fission de l’uranium 235 qui, en captant un neutron, se désintègre en un noyau de krypton, un de baryum et trois neutrons, l’énergie de liaison libérée équivaut à environ 1 Mégawatt-jour par gramme d’uranium fissionné. Les neutrons produits peuvent à leur tour être capturés et déclencher une réaction en chaîne : explosive, c’est la bombe A ; contrôlée, c’est l’énergie des centrales atomiques. En sens inverse, la fusion nucléaire, c-à-d. la fusion de deux noyaux légers en un noyau plus lourd (par exemple 1 deutérium + 1 tritium fusionnant pour donner 1 hélium + 1 neutron) produit une énergie encore plus considérable provenant de l’attraction entre nucléons due à la force de liaison : c’est le mécanisme à l’œuvre dans les étoiles… et la bombe H. Domestiquée, la fusion nucléaire donnerait une source d’énergie gratuite et illimitée.

A travers les deux exemples précédents, on comprend mieux l’intérêt pratique d’une meilleure connaissance de la force de liaison nucléaire, en fait ce qu’on appellera «l’interaction forte» en théorie quantique des champs (sections 5 et 6). Au plan scientifique plus général, la révolution einsteinienne a installé un nouveau paradigme, qui impose à toute théorie de la matière – et donc à toutes les théories quantiques – de se placer désormais dans le cadre du continuum espace-temps relativiste.

Les champs dynamiques

On va maintenant donner une illustration (qui n’est toujours pas une digression, mais dont on pourra reporter la lecture, en cas de surdose technique, jusqu’à avant la section 5) de la «relativisation» d’une théorie classique. Cet exemple n’est pas pris au hasard, mais se situe dans la perspective de la synthèse mécanique/électrodynamique recherchée. Rappelons (section 2) qu’à la fin du 19^ème siècle, grâce au recours aux méthodes statistiques, la mécanique rationnelle avait réussi à absorber la thermodynamique dans la théorie atomiste, le point matériel apparaissant comme l’idéalisation de l’atome. Mais la jonction avec la théorie ondulatoire apparaissait contre nature, à cause du dualisme, pour ne pas dire de l’antagonisme, entre ondes et corpuscules :

Propriétés macroscopiques des ondes et particules
	Particule	Onde
position ou interaction	localisée, d'extension définie	délocalisée, d'extension infinie dans le temps et l'espace
propagation	trajectoire continue, avec une vitesse définie et observable	diffusion en même temps dans toutes les directions (son "moment" virtuel n'est pas directement observable)
dénombrabilité et séparabilité	l'objet est dénombrable, et séparable en objets distincts.	l'objet est indénombrable et inséparable en objets distincts.

De fait, la synthèse ne pourra se faire qu’au milieu du 20^ème siècle (sections 4 et 5), mais ce long cheminement débute, comme on l’a signalé, avec l’irruption du concept de champ, qui a pris le pas sur le concept (si discutable) de force. La mécanique rationnelle avait en quelque sorte anticipé cette évolution en cédant progressivement la place à la mécanique analytique de Lagrange (à partir de 1788) et Hamilton (à partir de 1833), qui est une reformulation mathématique en termes de champs (au sens défini plus haut), bannissant carrément les notions de point matériel et de force dans l’étude d’un système dynamique.

Prenons un tel système S, formé de n points matériels M_i, n pouvant être infini (dans le cas d’un fluide par exemple). Classiquement, chaque point a 3 degrés de liberté (correspondant à sa position spatiale) et le système N = 3n degrés de liberté. Chaque point M_i possède aussi des paramètres dynamiques tels que sa quantité de mouvement, $\vec{q}_i = m.\vec{v}_i$ . L’idée de départ consiste à introduire un espace abstrait à N dimensions, appelé espace de configuration, puis un champ (au sens défini plus haut) dans cet espace de configuration, qu’on appellera champ dynamique du système S, et qui est censé décrire les états de S et leur évolution. Le premier champ de ce type est le Lagrangien $ \mathcal{L}(q_i,\dot{q}_i,t)$ (où $\dot{q}_i = \frac{dq_i}{dt}$ est la dérivée par rapport au temps), l’expression de cette fonction lagrangienne étant obtenue en général à partir de considérations sur les «symétries» de S. En mécanique classique, le Lagrangien n’est autre que ladifférence entre l’énergie cinétique et l’énergie potentielle. Il est crucial de noter l’espace de configuration est purement abstrait, ainsi que les fonctions q_i (appelées alors « coordonnées généralisées»), et donc que cette formalisation mathématisée est d’une portée très générale, permettant d’étudier toutes sortes de systèmes complexes. Les lois gouvernant la dynamique de S sont déduites d’un principe variationnel portant sur une fonctionaction définie comme l’intégrale du Lagrangien dans l’espace de configuration. Le principe de moindre action s’énonce alors :

«Parmi toutes les trajectoires possibles pour relier deux points de l’espace de configuration, celle qui est effectivement parcourue par le système est celle qui donne une valeur extrémale à l’action. »

De ce principe on déduit les équations du mouvement de Euler-Lagrange, qui contiennent celles de la mécanique rationnelle, de sorte que la mécanique lagrangienne apparaît comme une généralisation mathématique de la mécanique rationnelle d’où les notions de force et de point matériel ont été évacuées. La mécanique hamiltonienne est un perfectionnement formel de la lagrangienne, où les équations différentielles du second ordre de Euler-Lagrange sont avantageusement remplacées par les équations du premier ordre de Hamilton-Jacobi. Le nouveau champ dynamique est le Hamiltonien

$\mathcal{H} (q_i,p_i,t)=\sum\limits_k^N \dot{q}_kp_k-\mathcal{L}(q_i,\dot{q}_i,t) $

où $ p_i \equiv \frac{\partial \mathcal{L}}{ \partial\dot{q}_i}$ est appelé le moment conjugué de q_i.

En mécanique classique, le Hamitonien n’est autre que l’énergie totale, la somme des énergies cinétique et potentielle.

Encore une fois, il est important de noter que ce sont des définitions purement formelles, portant sur des champs généraux dans l’espace de configuration. On va immédiatement appliquer cette méthodologie au champ électromagnétique relativiste (et plus tard aux champs quantiques). La démarche est simple dans son principe.

Les champs électrique et magnétique classiques dérivent d’un champ potentiel électrique (scalaire) et d’un champ potentiel magnétique (vectoriel), qu’en théorie relativiste on doit regrouper en un seul quadrivecteur potentiel. Pour décrire la contribution à l’action des particules chargées circulant dans le champ électromagnétique, on construit un quadrivecteur courant dont les composantes sont la densité de charge et les trois composantes de la densité vectorielle de courant électrique, la loi de conservation du courant s’exprimant par la nullité de sa divergence. On calcule ensuite l’intégrale d’action invariante (par le groupe de Lorentz), qui comprend trois termes : le premier est un terme d’énergie cinétique associé à la propagation du champ électromagnétique en l’absence de charge ; le second est aussi un terme d’énergie cinétique associé à la propagation des particules chargées en l’absence de champ ; le troisième est un terme d’énergie potentielle associé à l’interaction du champ électromagnétique avec la matière. On en déduit, en appliquant le principe de moindre action, les équations (relativistes) de Maxwell ([CTS] p.88).

En résumé, on dispose avec le formalisme lagrangien d’une méthodologie systématique pour obtenir les équations d’évolution de systèmes divers, moyennant certaines adaptations et généralisations (mais c’est là le cœur du problème) adaptées à ces systèmes. Mais ce n’est qu’un formalisme, dont ne se satisfaisait pas Einstein, qui faisait valoir que «dans aucune autre théorie fondamentale, ne pouvaient coexister des points matériels dont la dynamique est régie par des équations différentielles ordinaires et des champs dont la mécanique est régie par des équations aux dérivées partielles » ([CTS] p.149), d’où ses essais obstinés, mais infructueux, de faire dériver le point matériel d’une théorie des champs. Cette quête ne devait finalement aboutir qu’avec la théorie quantique des champs (sections 5 et 6).

4-De la mécanique ondulatoire à la mécanique quantique

Ceci nous amène à un article d’Einstein sur la «Théorie quantique du rayonnement», où il observe que les quanta d’action du rayonnement électromagnétique portent non seulement de l’énergie, mais aussi, dans certaines conditions, un vecteur de quantité de mouvement. C’est le cas dans «l’effet Compton» (1923), où un photon (transporté par un rayonnement gamma) qui entre en collision inélastique avec un électron lui transfère non seulement de l’énergie mais de la quantité de mouvement : le photon diffusé a une énergie moindre, ce qui se traduit par un allongement de sa longueur d’onde, mais en même temps les trajectoires du photon et de l’électron diffusés divergent de celle du photon incident, suivant des angles qu’on peut calculer par la mécanique relativiste. Ainsi progresse l’idée d’une double nature de la lumière, à la fois ondulatoire et corpusculaire. Dans sa thèse de 1924, Louis de Broglie étend hardiment la dualité onde-corpuscule à n’importe quelle particule de l’univers microscopique, signant la naissance de la mécanique ondulatoire. Le raisonnement de de Broglie est à la fois quantique et relativiste.

Partant de l’hypothèse que la relation E = h.υ implique l’existence d’une fréquence «intrinsèque» υ associée à la particule étudiée, et sans se préoccuper du phénomène pulsatoire dont ce serait la fréquence, il cherche à relier la longueur d’onde λ à la quantité de mouvement (relativiste) de la particule. On rappelle que pour une onde, le produit λ.υ est la «vitesse de phase», notée v_φ. Pour calculer celle-ci, de Broglie pose un principe «d’harmonie des phases» selon lequel «le phénomène périodique de fréquence υ’ dans le référentiel propre de la particule est constamment en phase avec une onde se propageant dans la même direction que le mobile» [une onde-pilote en quelque sorte]. Dans le cas d’une particule de masse (au repos) m, en mouvement rectiligne uniforme de vitesse v, une simple application des définitions et de la transformation temporelle de Lorentz montre que v.v_φ = c² et que υ = γ.υ’, où γ est le facteur relativiste habituel, $1/ \sqrt{1-v^2/c^2}$. Comme E = h.υ = γ.mc², on en déduit immédiatement la formule de de Broglie, λ.p = h, où p est la quantité de mouvement relativiste.

Commentaire d’Einstein : «De Broglie a levé un coin du voile». En 1927, l’expérience «critique» de Davisson et Germer qui obtiennent, en bombardant une cible de nickel cristallin par des électrons lents, une figure de diffraction (fig. 4.1, fig. 4.2) confirmant la dualité onde-corpuscule, apportera à de Broglie le prix Nobel de physique en 1929. En 1931, le microscope électronique, où les photons sont remplacés par des électrons, fait entrer la mécanique ondulatoire dans le domaine pratique. Mais les théoriciens n’ont pas attendu cette confirmation pour se lancer à corps perdu dans la refondation quantique de la mécanique. «Le corpus de la mécanique quantique, formalisme et interprétation, a été élaboré en 1925 et 1926 par une poignée de jeunes chercheurs brillants venant des quatre coins d’une Europe que la guerre venait de déchirer et qui ont, en quelques années, construit l’une des plus extraordinaires réalisations de l’esprit humain» (M. Crozon). L’une des plus déconcertantes aussi, tant elle s’éloigne de l’intuition commune, au point de provoquer encore aujourd’hui, malgré ses succès éclatants, des débats épistomologiques sans fin.

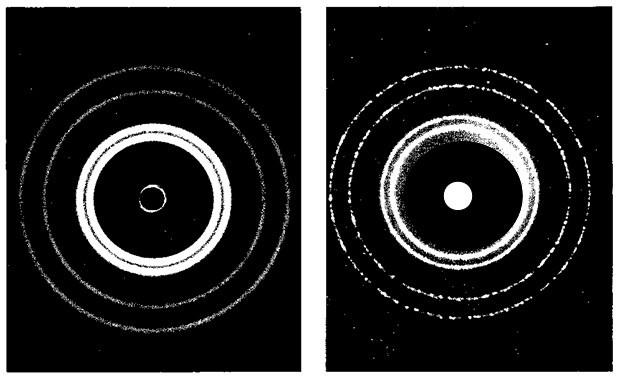
Fig. 4.1 Diffraction du rayonnement X (gauche), et diffractiond’électrons (droite)

Fig. 4.2 Diffraction d’électrons

La mécanique ondulatoire n’est pas encore devenue la mécanique quantique quand Erwin Schrödinger s’attaque à l’équation d’évolution de la fonction d’onde de de Broglie. Son idée de départ, tout à fait conforme à la dualité onde-corpuscule, consiste en une analogie formelle entre optique et mécanique, plus précisément entre le principe variationnel de Fermat en optique géométrique (la lumière se propage d’un point à un autre sur une trajectoire dont la durée de parcours est localement minimale) et le principe de moindre action en mécanique analytique (équation de Hamilton-Jacobi). Face à de sérieuses difficultés techniques, il se résigne à se restreindre au cadre non relativiste, et il obtient en 1926 la célèbre équation linéaire aux dérivées partielles qui porte son nom :

$i\hbar\frac{\partial\Psi(t,\vec{r}\,)}{\partial t}=-\frac{\hbar^2}{2m}\vec{\Delta}^2\Psi(t,\vec{r}\,)+V(t,\vec{r}\,)\Psi(t,\vec{r}\,)$

$\frac{\hat{\vec{\mathbf{P}}\,}^2}{2m}|\Psi(t)\rangle+V(\hat{\vec{\mathbf{r}}},t)| \Psi(t)\rangle=i\hbar\frac{\mathrm{d}}{\mathrm{dt}}|\Psi(t)\rangle $

$ (i\hbar\frac{\partial \mathit{\Psi}}{\partial t}(\mathbf{x},t)= \left( mc^2\alpha_0 - i\hbar c\sum\limits_{j=1}^{3}\alpha_j\frac{\partial{}}{\partial{x_j}}\right)\mathit{\Psi}(\mathbf{x},t)$

La première équation est l’équation non relativiste de Schrödinger ; la seconde est la même, mais écrite en termes d’opérateurs agissant sur des vecteurs d’état (voir plus loin) ; la troisième est l’équation relativiste de Dirac, écrite aussi en termes d’opérateurs

Schrödinger ne pouvait pas parvenir à une équation relativiste sans utiliser la notion de spin (tourner comme une toupie, en anglais) d’une particule. Deux versions relativistes furent par la suite élaborées, par Klein et Gordon en 1926 pour les particules de spin 0 (comme… le boson BEH), par Dirac en 1928 pour celles de spin ½ (comme l’électron). Ce second travail contenait aussi comme corollaire – si l’on peut appeler ainsi une découverte aussi renversante – l’existence de l’anti-matière. La mise en évidence par Anderson en 1932 de l’anti-électron (ou positon) dans le rayonnement cosmique devait valoir à Dirac le prix Nobel de physique 1933 (partagé avec Schrödinger). Suggéré par Pauli, mis en forme théorique par Goudsmit et Uhlenbeck en 1925, le spin représente intuitivement le moment cinétique propre d’une particule tournant sur elle-même. Ce degré de liberté supplémentaire s’ajoutant aux trois degrés spatiaux habituels devait pallier les insuffisances du modèle de Bohr.

Mais l’intuition s’arrête là, car Pauli lui-même a montré en 1924 qu’une particule de la taille de l’électron et tournant comme une toupie devrait avoir une vitesse tangentielle supérieure à c ! De fait, bien que le spin soit une caractéristique physique au même titre que la masse ou la charge, c’est aussi un paramètre quantique (on dit nombre quantique, section 5) prenant des valeurs discrètes (entières ou demi-entières), sans équivalent classique, contrairement, par exemple, à la position, l’impulsion, l’énergie… On touche ici du doigt la puissance des concepts quantiques, mais aussi la difficulté à les vulgariser : les principes échappent à l’intuition commune, le langage mathématique à la compréhension ordinaire, et pourtant les résultats sont là !

Le spin joue un rôle important dans les phénomènes de magnétisme et de polarisation. Le fait que le spin de l’électron soit égal à + ou – ½ (au lieu du signe, les anglo-saxons préfèrent dire «up» et «down», i.e. «pôle Nord en haut ou en bas») explique la structure fine des raies de l’hydrogène ainsi que l’expérience de Stern-Gerlach. Mieux, le spin se manifeste dans des applications de tous les jours dont l’homme de la rue bénéficie sans en soupçonner l’origine : la manipulation des spins nucléaires par résonance magnétique nucléaire a bouleversé les techniques de spectroscopie (RMN) et d’imagerie médicale (IRM) ; celle des courants de spins dans des nano-circuits a donné naissance à la «spinotronique», qui a permis l’explosion des mémoires des USB, MP3, smartphones et autres gadgets, et dont le prix Nobel récompensant Albert Fert en 2007 a en quelque sorte officialisé l’existence…

La mécanique quantique a pour ambition de fournir un cadre général pour décrire le comportement des particules à l’échelle atomique. On la distinguera arbitrairement de la mécanique ondulatoire par son formalisme théorique, inspiré de la mécanique analytique et développé autour des années 1930 principalement par Heisenberg, Dirac, et «l’école de Copenhague» autour de Bohr – un formalisme fécond, mais, pour une théorie qui se propose de décrire le monde physique, d’une abstraction jamais égalée, sauf peut-être par la relativité générale. A en croire leur biographie, Dirac et Heisenberg étaient pour ainsi dire des «mathématiciens contrariés», ce n’est donc pas un hasard si la présentation faite par Dirac en 1930 des principes de la mécanique quantique s’appuie sur une théorie tirée de l’analyse fonctionnelle, celle des espaces de Hilbert et des opérateurs hermitiens. On remarquera encore une fois «la déraisonnable efficacité des mathématiques». La notion de «vecteur» étant intuitivement acquise, on demandera au lecteur de bien vouloir admettre que non seulement les vecteurs s’additionnent, mais peuvent aussi se multiplier par des scalaires qui sont des «nombres complexes», fabriqués à partir des nombres réels en ajoutant une racine carrée de –1 (notée i, donc i² = –1).

Un espace de Hilbert est un espace de vecteurs de dimension infinie (avec un nombre infini de degrés de liberté) muni d’un produit scalaire (un produit entre vecteurs prenant des valeurs complexes) défini comme étant un accouplement sesquilinéaire, non dégénéré… qu’il n’est pas utile d’expliquer ici. Un opérateur hermitien de cet espace est une transformation sur ses vecteurs qui respecte les lois de composition des vecteurs, mais aussi une certaine propriété de symétrie (qu’on ne détaillera pas). Exprimés de façon générale, c-à-d. en évitant toute référence à la nature du système physique étudié, les 6 postulats de la mécanique quantique s’énoncent ainsi :

Les états d’un système de particules en nombre fini fixé sont représentés par des vecteurs d’un espace de Hilbert , appelés vecteurs d’état ou fonctions d’onde, et généralement notés |x> (c’est la notation «bra-ket» de Dirac)
Les propriétés observables du système sont représentées par des opérateurs hermitiens de l’espace de Hilbert, appelés simplement des observables. Exemples : l’opérateur d’énergie potentielle V, l’opérateur d’énergie cinétique K, l’opérateur d’énergie totale, ou hamiltonien, H = K + V
La mesure d’une grandeur physique représentée par un observable A ne peut être qu’une valeur propre de cet opérateur. On rappelle qu’un vecteur propre |x> de A associé à une valeur propre a doit vérifier A.|x> = a.|x>. Les valeurs propres d’un opérateur hermitien sont toujours des nombres réels
Tout opérateur hermitien possède un système complet de vecteurs propres e_n, tels que tout vecteur |x> de H s’écrit de façon unique sous la forme d’une somme infinie convergente de termes a_n.|e_n>. Si cette somme représente le vecteur d’état |x> (normalisé) immédiatement avant la mesure, la probabilité pour que la mesure donne a_n est égale à |a_n|², le carré du module de a_n. Cet axiome probabiliste est dû à Max Born (prix Nobel 1954)
Immédiatement après la mesure, le vecteur-état devient un vecteur propre correspondant à la valeur propre donnée par la mesure («réduction du paquet d’onde», ou «collapse» en anglais)
L’état de tout système quantique non relativiste est une solution de l’équation de Schrödinger dépendant du temps ; autrement dit, c’est le hamiltonien qui régit l’évolution du système dans le temps.

Niels Bohr avait coutume de dire : «Quiconque n’est pas choqué par la théorie quantique ne la comprend pas». De fait, la première réaction du profane devant les 6 axiomes se résume naturellement en une exclamation : «Abracadabradantesque!» Pour le non profane, c’est bien sûr le postulat probabiliste de Max Born qui pose problème. Sans entrer dans la polémique épistomologique, contentons-nous d’examiner de plus près quelques corollaires notoires de l’axiome 4 :

Le principe d’indétermination de Heisenberg

Le postulat 1 donne une expression axiomatique de la dualité onde-corpuscule en proposant, puisqu’un objet quantique a une certaine extension (dans l’espace) et une certaine durée (dans le temps), de le représenter non plus par un ensemble de valeurs scalaires (coordonnées de position, de vitesse) mais par une fonction d’onde décrivant sa distribution spatio-temporelle (voir fig. 4.3). Mais intuitivement, une particule est «ici ou là», tandis qu’une onde est «partout», et la formule de de Broglie reliant l’impulsion à la fréquence (voir plus haut) porte déjà en germe un principe d’indétermination : par exemple, pour une fréquence donnée, seule l’impulsion est déterminée, c-à-d. le produit de la masse par la vitesse, pas la vitesse et la masse individuellement.

Dans le formalisme quantique, Heisenberg (prix Nobel 1932) explique ce type d’indétermination par la «non commutation» des (opérateurs représentant les) observables. En effet, par définition même, le produit de deux opérateurs n’est pas forcément commutatif, c-à-d. que A.B peut être différent de B.A ; la différence, appelée le «commutateur», noté [A, B], mesure le défaut de commutativité. Pour les observables de position $\hat{x}$ et d’impulsion $\hat{p}$, l’équation de Schrödinger entraîne que le commutateur [$\hat{x}$, $\hat{p}$] est égal à iħ, où ħ est la constante de Planck normalisée. Le postulat 4 implique alors qu’on ne peut pas mesurer simultanément avec précision la position et l’impulsion, ou plutôt que le produit des écarts-type de ces mesures doit être supérieur ou égal à ħ/2. Une incertitude analogue touche le couple énergie-temps, le produit des écarts-type devant être supérieur ou égal à ħ. En termes d’opérateurs, Heisenberg pose en 1927 son principe d’indétermination général (il s’agit en fait d’un théorème, démontré à partir des axiomes quantiques) sous la forme :

$\Delta A \cdot \Delta B \geq \frac{1} {2} | \langle [ \hat{A},\hat{B}] \rangle_\gamma |$

où A et B sont deux observables, $\hat{A}$ et $\hat{B}$ les opérateurs correspondants,

$\langle\rangle_\gamma$ est la moyenne sur l’état $|\gamma\rangle$

Δ X est l’écart type de X : $ \sqrt{\langle \hat{X}^2\rangle_\gamma-\langle \hat{X} \rangle^2_\gamma } $

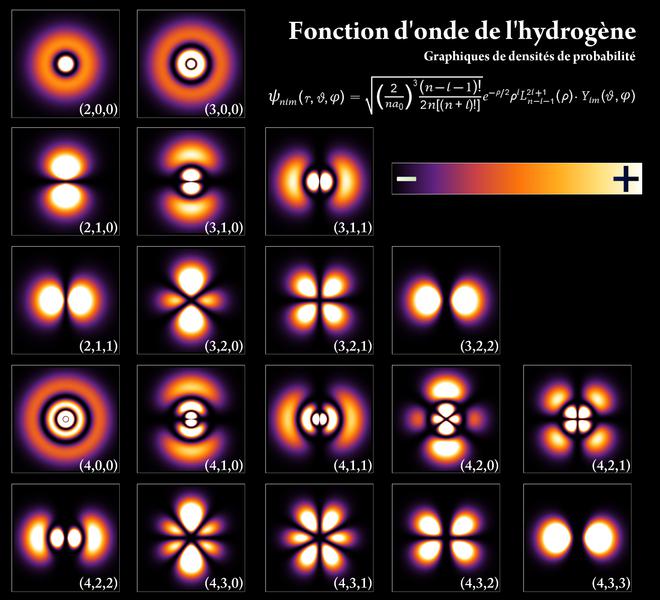
Fig. 4.3 Fonction d’onde de l’hydrogène avec densité de probabilités

Physiquement, cette inégalité signifie qu’à cause du quantum de Planck, toute amélioration de la mesure sur un observable se fait au détriment de la précision sur l’autre. Il est important de souligner que le principe de Heisenberg ne porte pas sur la mesure subjective des grandeurs (dépendant par exemple des instruments), mais sur une impossibilité fondamentale de les déterminer. C’est pourquoi il est préférable de parler de principe d’indétermination plutôt que d’incertitude. En tout cas, entre indétermination et déterminisme, le débat épistémologique fait rage. On connaît bien la formule d’Einstein : «Dieu ne joue pas aux dés», peut-être moins bien la réplique de Niels Bohr : «Qui êtes-vous, Einstein, pour dire à Dieu ce qu’il doit faire ou pas?»

Le chat de Schrödinger

Comme deux vecteurs peuvent s’additionner, l’axiome 1 et la linéarité de l’équation de Schrödinger dans l’axiome 4 permettent à deux états queconques, dans le langage des physiciens, de se superposer. Mais ce «principe de superposition», combiné aux principes quantiques de la mesure (axiomes 2 à 4), engendre des paradoxes quand on superpose des états contradictoires. Pour illustrer de façon amusante le paradoxe d’un état qui s’écrirait :

$(1/ \sqrt{2}).(|mort\rangle + |vivant\rangle)$

(où le scalaire multiplicateur sert seulement à normaliser les vecteurs, de façon à ce que les probalités restent toujours inférieures ou égales à 1), Schrödinger a imaginé une «expérience de pensée» consistant à enfermer un chat dans une boîte, avec un dispositif (un flacon d’acide cyanhydrique pour Schrödinger, un baril de poudre pour Einstein) qui tue l’animal dès qu’il détecte la désintégration d’un atome d’un corps radioactif (fig.4.4). En supposant que l’atome a 1 chance sur 2 de se désintégrer au bout d’une minute, le chat est-il mort ou vivant au bout d’une minute ? D’après les principes quantiques de la mesure, tant que l’observation n’est pas faite, l’atome est dans un état superposé, en quelque sorte simultanément intact/désintégré, et donc le chat est simultanément vivant/mort jusqu’à ce que l’ouverture de la boîte déclenche le choix entre les deux états (axiome 2). Bref, ce n'est pas qu' on ne sait pas répondre à la question sans ouvrir la boîte pour voir, mais que la réponse n'est pas dans la boite tant qu'on ne l'a pas ouverte !!!

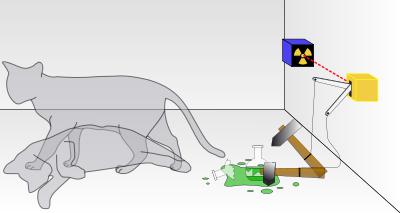
Fig. 4.4 Le chat de Schrödinger

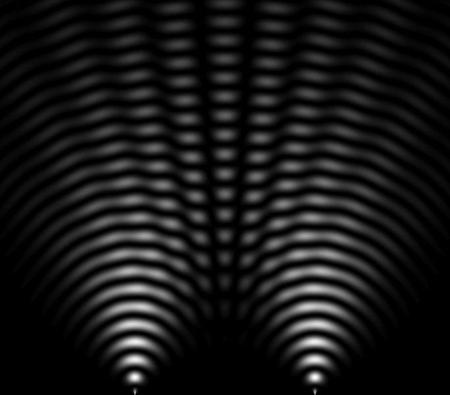
En fait, une expérience analogue à l’expérience de pensée avec le «chat-zombie» de Schrödinger peut être réalisée en pratique, celle des fentes de Young. En 1801, ç’avait été une des expériences «critiques» qui avaient fait pencher la balance en faveur de la nature ondulatoire de la lumière (voir section 3) : en éclairant avec une seule source de lumière un plan opaque percé de deux étroites ouvertures, on obtient de l’autre côté deux faisceaux lumineux qui interfèrent et donnent sur un écran des «franges d’interférence» où alternent des zones sombres et illuminées (fig. 4.5). La même manipulation effectuée avec des faisceaux de particules donne aussi des interférences, alors qu'on s'attendrait à voir les particules simplement s'accumuler derrière les fentes. Mieux, si , comme le permettent les techniques modernes, on envoie non plus des jets mais des particules isolées (photons ou électrons), on observe à nouveau des interférences comme dans l’expérience originelle de Young. L’interprétation quantique, comme pour le chat de Schrödinger, est que la particule, se trouvant dans un état superposé, est «passée par les deux ouvertures en même temps».

L’effet tunnel, utilisé dans le «microscope à effet de champ» (fig. 1.1 & fig. 1.2 chap. 1) relève de la même problématique. C’est l’effet par lequel un objet quantique peut franchir une barrière de potentiel même si son énergie totale est inférieure à l’énergie minimale requise. De fait, en rencontrant la barrière, la fonction d’onde s’affaiblit exponentiellement mais ne s’annule pas (c’est le phénomène des «ondes évanescentes» en électromagnétisme), de sorte qu’il existe une probabilité, faible mais non nulle, de retrouver la particule de l’autre côté de la barrière.

44b

Fig. 4.5 Expérience des fentes de Young

Les particules isolées passant par les fentes donnent le même type d’interférences que les rayons lumineux

Fermions vs. Bosons

C’est seulement maintenant que nous sommes en mesure de donner la définition d’un boson. L’appellation vient du nom de Satyendranath Bose, un physicien indien avec qui Einstein développa dans les années 1920 une statistique quantique des photons. Les physiciens s’étaient aperçus que la statistique classique de Boltzmann ne s’appliquait pas de la même manière à toutes les particules, ce qui affectait de façon très importante le décompte des configurations pour calculer l’entropie. Les statistiques quantiques de remplacement sont liées au phénomène d’indiscernabilité quantique de particules identiques ([CTS] p.176).

Prenons par exemple deux particules identiques 1 et 2 pouvant se trouver dans deux états quantiques a et b, et notons |ψ₁> et |ψ₂> les deux configurations {1 en a, 2 en b} et {1 en b, 2 en a}. Comme |ψ₁> et |ψ₂> sont indiscernables, le postulat 4 implique que leurs amplitudes de probabilité sont des nombres complexes de même module, c-à-d. que le quotient q de ces deux amplitudes est de module 1 ; en permutant les rôles des deux particules, on voit que q² = 1, c-à-d. q = +1 ou -1.

Si q= +1, on dit que les particules sont des bosons (ex. : des photons) ; si q = -1, que ce sont des fermions (ex. : des électrons). On peut démontrer mathématiquement que les fermions un spin demi-entier et les bosons un spin entier (théorème fondamental de la connexion spin/statistique). Pour dire les choses de façon pittoresque, les particules se divisent ainsi en deux clans, les «individualistes», qui nous empêchent de traverser les murs, et les «grégaires», qui nous aveuglent de leur lumière. Plus scientifiquement, les fermions obéissent à la «statistique de Fermi-Dirac» : si q = -1 et a = b, on voit tout de suite que |ψ₁> = 0, autrement dit deux fermions identiques ne peuvent (probablement) pas se trouver au même endroit dans le même état quantique ; c’est le «principe d’exclusion de Pauli», qui explique en particulier l’impénétrabilité de la matière, puisque protons, neutrons et électrons sont des fermions. Les bosons quant à eux obéissent à la statistique de Bose-Einstein : ils tendent à se regrouper dans l’état quantique de plus basse énergie, où leurs amplitudes de probabilité tendent à s’additionner ; c’est le «condensat de Bose-Einstein», qui explique en particulier «l’émission stimulée» de photons (déjà signalée par Einstein dans son article cité au début de cette section), à l’origine de l’effet laser.

La «déraisonnable efficacité» des principes quantiques pose les mêmes problèmes épistémologiques que ceux effleurés dans la section 3 à propos d’autres théories scientifiques. L’attitude qui semble prévaloir majoritairement est «l’empirisme» de l’école de Copenhague, que Stephen Hawking résume ainsi dans ses bons jours : «Je ne demande pas qu’une théorie corresponde à la réalité, car je ne sais pas ce qu’est la réalité. Ce n’est pas quelque chose que l’on peut tester avec du papier pH [papier réactif qui change de couleur suivant le pH du milieu où il est plongé]. Tout ce qui m’importe est que la théorie prévoie correctement le résultat d’une expérience». Et dans ses mauvais jours : «Quand je vois le chat de Schrödinger, je sors mon revolver».