Về vật chất - III
Tất cả
những gì bạn vẫn muốn
biết từ
lâu về vật chất,
nhưng còn
ngại hỏi – Phần-III
Nguyễn Quang
5- Từ RQM tới QFT (i)
Mặc dù đã đạt nhiều thành quả, cơ học lượng tử tương đối tính (RQM) vẫn chịu một khiếm khuyết quan trọng : Trước khi có công trình « lượng tử hoá lần thứ hai » do Dirac tiến hành, lý thuyết RQM chỉ có thể mô tả các hệ thống gồm một số vi hạt nhất định, không đổi và không tương tác với nhau ; đặc biệt là cơ chế đầy đủ của các tiến trình sinh và diệt của vi hạt hoàn toàn nằm ngoài lý thuyết, ngay trong khi mà việc kết hợp cơ học lượng tử và thuyết tương đối của Dirac đã mang đến phản-vật-chất. Cần phải lấp khoảng trống ấy, dù chỉ là để sắp xếp cái sở thú những hạt « cơ bản » (có đến hơn 400, vào đầu những năm 1950) ngày càng thấy nhiều cùng với sự phát triển các máy gia tốc ngày càng mạnh, về chuyện này Enrico Fermi đã khôi hài : « nếu tôi có thể nhớ hết tên những thứ trong cái chuồng này, tôi có lẽ nên làm người gác sở thú, chẳng nghiên cứu vật lý làm gì ! » (bảng 5.1). Không phải vì thế mà người ta không có thể áp dụng phương pháp sơ đẳng nhất trong các khoa học tự nhiên, đó là sự phân loại, để có thể làm lộ ra một cách thử nghiệm những cấu trúc tiềm ẩn của chúng (như Mendeleïev đã thực hiện trong bảng tuần hoàn các đơn chất). Việc nghiên cứu « lực liên kết » trong lõi nguyên tử và sự phân rã bêta làm cơ sở đưa đến ý tưởng rằng, ngoài hai loại tương tác được biết đến trong vật lý học cổ điển là tương tác hấp dẫn và tương tác điện từ, sẽ rất thuận tiện nếu ta thêm vào hai loại tương tác mới nữa : tương tác mạnh và tương tác yếu, mà cường độ và phạm vi hoạt động được tóm tắt trong bảng 5.1.
Xin để ý điều làm cho người ta gán thêm tính từ (mạnh hay yếu) cho tên gọi của hai loại tương tác này, đúng là vì cường độ của chúng, nhưng cũng vì xác suất xuất hiện nữa : xác suất làm nảy sinh phản ứng hạch nhân khi bắn một chùm vi hạt alpha vào một lõi nguyên tử (như trong thí nghiệm của Rutherford) là mạnh ; xác suẩt phân rã xẩy ra trong hiện tượng phóng xạ bêta thì yếu hơn, điều này được chứng minh qua việc nửa tuổi đời của nơtron nằm trong quãng thời gian vĩ mô (khoảng 15 phút). Tập hợp bốn tương tác cơ bản được coi như chi phối và giải thích được tất cả các hiện tượng vật lý mà con người biết đến, trong đó người ta biết rằng lực hấp dẫn trở nên không đáng kể ở kích cỡ nguyên tử hay hạ nguyên tử. Một phân loại đầu tiên chia ra ba nhóm : photon, chịu tác động của tương tác điện từ ; các hadrons, chịu tương tác mạnh ; và leptons, chịu tương tác yếu, cũng như lực tương tác điện từ (trừ nơtrinô). Rồi các vi hạt chịu tương tác mạnh lại được chia thành hai nhóm nhỏ theo spin của chúng: các baryons (nặng) với spin = 1/2 hay 3/2, và các mésons (trung bình) với spin = 0 hay 1.
Việc phân loại tinh tế hơn nữa có lên hệ đến các số lượng tử, nghĩa là trị số riêng của các toán tử giao hoán được với trường Hamilton (xem chương 3), và có vai trò xác định những tính chất bất biến trong vận động của vi hạt : trong đó có spin, nhưng còn có « sắc-tính », « duyên-tính », « vị-tính », « kỳ-tính »(ii)... Hiển nhiên, người ta nghi rằng trong cái danh mục giống như một bài thơ siêu thực này, nhiều vi hạt « cơ bản » là không cơ bản, và có nguồn gốc từ những quá trình tương tác giữa một số ít hơn các vi hạt thực sự cơ bản. Đó là điều mà bảng 5.3 cho thấy, bảng này tóm lược các thành tố tối hậu (cho đến nay) của vật chất và các tương tác giữa chúng, và trong đó boson BEH cuối cùng cũng có chỗ của nó.
| Tương tác | Lý thuyết hiện hành | Trung gian |
Khối lượng (GeV/c2) |
Công suất tương đối | Bán kính vùng tác động (m) | Biến thiên theo khoảng cách |
| Mạnh |
Sắc động học lượng tử (QCD) |
8 gluons | 0 | 1 | 2,5·10−15 | \(\frac{1} {r^7}\) |
| Điện từ | Điện từ học lượng tử (QED) | photon | 0 | 10-2 | ∞ | \(\frac{1} {r^2}\) |
| Yếu | Lý thuyết điện yếu | W+, W-, Z0 | 80, 80, 91 | 10-13 | 10−18 | từ \(\frac{1} {r^5}\) đến \(\frac{1}{r^7}\) |
| Hấp dẫn | Thuyết tương đối rộng |
graviton (giả định) |
0 | 10-38 | ∞ | \(\frac{1} {r^2}\) |
Bảng 5.1 Tóm lược bốn tương tác cơ bản

Bảng 5.2 Các vi hạt cơ bản trong những năm 1950

Bảng 5.3 Các vi hạt cơ bản trong mô hình chuẩn
Nhưng, như chúng tôi đã báo trước với độc giả, vén lên quá sớm bức màn của hồi kết sẽ chỉ đem lại hàng loạt câu hỏi – thực ra đó sẽ là tất cả những câu hỏi mà lý thuyết trường lượng tử (QFT) sẽ phải giải quyết. QFT là lý thuyết hậu duệ của lý thuyết RQM (Relativistic quantum mechanics – Cơ học lượng tử tương đối tính) sau khi đã trải qua những dạng thức tiếp nối / bổ sung ; từ QED (quantum electrodynamics, điện động học lượng tử) cho đến QCD (quantum chromodynamics, sắc động học lượng tử), từ đối xứng chuẩn cho đến sự phá vỡ tự phát đối xứng. Chính ở đây chúng tôi đã đụng phải giới hạn của khả năng phổ biến khoa học, bởi vì, khi các khái niệm không còn có điều tương tự trong vật lý học cổ điển (thí dụ như các số lượng tử), chỉ còn ngôn ngữ toán học là có thể dùng để định nghĩa chúng một cách chính xác. Ngôn ngữ của trực giác còn giữ được khả năng gợi ý, nhưng giá phải trả là sự mơ hồ, và đôi khi sự lẫn lộn đến từ những suy luận dựa trên những tương tự giả tạo.
Cuộc lượng tử hoá lần thứ nhì
Trước khi lại chồng chất thêm vài tiên đề lên trên sáu định đề đã đề cập trong chương 4, tưởng cũng nên xem xét, do giá trị khai phá của chúng, hai phác thảo đầu tiên nhằm mô tả các tương tác yếu và mạnh, lần lượt do Fermi và Yukawa đề nghị trong các năm 1934 và 1935 :
– Trong hiện tượng phóng xạ bêta, một nơtron biến thành bộ ba proton + điện tử + nơtrinô, cặp proton + điện tử đảm nhận sự bảo toàn điện tích và cặp proton + nơtrinô đảm nhận sự bảo toàn khối lượng. Xin nhớ là vào lúc ấy, nơtrinô chỉ là một vi hạt giả định, do Pauli sáng tạo ra, có một khối lượng cực kỳ nhỏ (nhưng khác không) do đó thật sự đặc biệt khó phát hiện ; nó chỉ được làm lộ diện vào năm 1956. Những giải thích đầu tiên về cơ chế phóng xạ bêta đều hiểu ngầm là điện tử đã nằm sẵn trong lõi nguyên tử. Đoạn tuyệt hẳn với định kiến đó, trong mô hình do Fermi (giải Nobel 1938) đề nghị thì cả điện tử lẫn nơtrinô đều không hiện hữu trước, chúng được tạo ra trong một tương tác « đụng độ » giữa bốn fermions, nói chính xác hơn là giữa hai cặp fermions - phản-fermions. Thuyết của Fermi có thể được coi như một tiệm cận gần đúng (trường hợp năng lượng thấp) của QED, lý thuyết thống nhất hai lực điện từ và yếu trong mô hình chuẩn, với điều kiện thay thế các tương tác « đụng độ » bằng các tương tác trao đổi, qua một bộ ba bosons W trung gian (xem dưới đây).
– Vừa hay, mô hình do Yukawa (giải Nobel 1949) đề nghị đã giải thích tính kết cấu chặt của lõi nguyên tử bằng tương tác giữa các nucléons qua sự trao đổi một vi hạt giả định, được đăt tên là meson π , hay pion, với khối lượng bằng 200 lần khối lượng điện tử, và vi hạt này được phát hiện năm 1947. Trong lý thuyết QCD của mô hình chuẩn, meson là lượng tử của trường tương tác mạnh. Khi được trao đổi, vi hạt này trở thành không định xứ, có phần giống như con mèo của Schrödinger, và định đề « giảm sóng » có hệ luận là nếu đã phát hiện ra nó thì sự trao đổi giữa hai nucleons trong cuộc đã bị gián đoạn. Nguyên lý bất định của Heisenberg khi đó cho phép người ta xác định các giới hạn của biến đổi năng lượng (tức cũng là khối lượng) và của thời gian di chuyển vi hạt - năng lượng đó (xem chương 2), hình thành một « cái hộp » mà kích thước được xác định bởi hằng số Planck. Như thế là, từ kích thước của nguyên tử, Yukawa đã có thể ước tính khối lượng của meson π.
Hai phác thảo nói trên của QFT làm hiện rõ nguyên lý về sự sinh / diệt của một số vi hạt trong sự tương tác giữa các trường. Đây cũng là một cách trả lời cho ước vọng thống nhất trường và hạt của Einstein (đã được nhắc đến tại cuối chương 3) : « Dưới dạng đã chín muồi của nó, ý tưởng của thuyết QFT cho rằng các trường lượng tử là chất liệu cơ bản của vũ trụ, và rằng các hạt chỉ là những gói năng lượng và mômen của các trường đó […] lý thuyết QFT như vậy đã đưa đến một quan niệm thống nhất hơn về tự nhiên so với cách diễn tả lưỡng tính cũ, dùng đến cả hai khái niệm hạt và trường » (S. Weinberg, giải Nobel 1979).
Đã đến lúc trình bày dạng thức của công trình « lượng tử hoá lần thứ hai », mà, như chúng tôi đã nhắc đến, sự khiếm khuyết của một ngôn ngữ không toán học làm cho diễn ngôn trở thành mơ hồ và sơ sài hơn các đoạn trước.
Bước đầu tiên có nội dung diễn tả những dữ kiện về các vectơ trạng thái và về các khả-lượng (xem chương 4) như những dữ kiện về các trường, được xác định cho mỗi điểm trong không-thời-gian, theo ý nghĩa trong chương 3. Trong mọi trường hợp, chúng ta sẽ gọi tên chúng là các trường lượng tử. Từ đó ta ghi nhận rằng nguyên lý song trùng của RQM (định đề 1) từ một khởi đầu tuỳ tiện, trở thành tự nhiên, bởi vì theo chính định nghĩa của chúng, các trường có thể song trùng. Ở bước thứ nhì cần được đưa thêm vào các toán tử trường ; để thuận tiện về mặt toán học, người ta không định nghĩa chúng trong không thời gian, mà bằng khái niệm mômen liên hợp trong không gian cấu hình (xem chương 3). Có thể nói, theo một nghĩa nào đó, rằng trong khi RQM đã lượng tử hoá cơ học thuần lý, thì QFT sẽ lượng tử hoá cơ học phân tích. Các mômen liên hợp của dạng thức toán học Lagrange được thay thế bằng các toán tử đại diện cho những khả lượng, như trong RQM, và chúng sẽ tuân thủ các hệ thức giao hoán (xem chương 4) tuỳ theo, dĩ nhiên, việc diễn tả vật lý của các momen đó.
Một khó khăn chuyên môn : làm sao xác định không gian Hilbert trên đó các toán tử trường thao tác ? Bởi vì các vi hạt trong hệ thống được nghiên cứu có nhiều loại, lại có số lượng thay đổi, không gian quy chiếu phải bao gồm đủ các không gian trạng thái của chúng, lại còn cần phản ảnh những đặc tính thống kê khác nhau trong vận động của chúng (Bose-Einstein hay Fermi-Dirac).
Trong vật lý học thống kê đã có sẵn một không gian thích hợp, không gian Fock. Khi được áp dụng vào trong khung cảnh lượng tử, nó trở thành một sự bội trùng(iii) vô tận (về mặt toán học, đó là một tổng trực tiếp của các tích tenxơ) của tất cả mọi không gian trạng thái của các vi hạt trong hệ thống, trên đó được người ta tác động bằng một toán tử nhằm đối xứng hoá hay phản đối xứng hoá chúng, tuỳ theo chúng là bosons hay fermions. Không gian Fock được lượng tử hoá bởi các số chiếm hữu, hợp thành một cơ sở thuận tiện cho nó, và được định nghĩa như sau : trong một không gian trạng thái nhất định của một tập hợp các vi hạt đồng nhất, chấp nhận một cơ sở \(|\psi_j\rangle\), con số chiếm hữu |n0, n1,…, nk> chỉ định trạng thái tương ứng với n0 vi hạt trong trạng thái \(|\psi_0\rangle\),…, nk vi hạt trong trạng thái \(|\psi_k\rangle\). theo quy ước, \(|0\rangle\) chỉ định trạng thái «rỗng», tức là trạng thái của mức năng lượng thấp nhất (chứ không phải hư vô!).
Không gian Fock là không gian biểu diễn của hiện tượng học lượng tử, các toán tử trường sẽ tác động trên không gian này để tạo ra các sự kiện, đó chính là phát ra hoặc hấp thụ một lượng tử trường ([CTS] tr.162). Do vậy, về mặt toán học, các toán tử này nằm trong cấu trúc algebra phát sinh từ hai toán tử diệt và sinh, có ký hiệu viết theo thứ tự \(a\) và \(a^\dagger\), chúng là những toán tử phụ hợp trong nghĩa toán học, và tác động trên một trạng thái Fock bằng cách thêm hoặc bớt đi một vi hạt. Đặc biệt là, trong cơ sở gồm các số chiếm hữu, toán tử diệt ai tác động trên |n1,…, nk> bằng cách biến đổi ni thành ni + 1 và không thay đổi các toạ độ khác. Các toán tử của cấu trúc algebra từ đó có thể được biểu diễn bằng các toạ độ \(a_i\) và \(a_j^\dagger\), một cách trực tiếp hay thông qua phép biến đổi Fourier. Trong trường hợp đơn giản của một « trường tự do » (nghĩa là không có tương tác) của các bosons chẳng hạn, trường Hamilton (trong đó Ek là động năng) được viết như $$H=\sum_kE_ka_k^\dagger a_k,$$ và toán tử diệt của các bosons (trong đó r là vectơ vị trí và k_i là một vectơ sóng) là :$$\phi(\mathbf{r}) \equiv \sum_ie^{k_i.r}a_i.$$
Trong một tương tác giữa các trường, việc chuyển đổi từ không gian Fock các trường tự do đầu vào sang không gian Fock các trường tự do đầu ra được mô tả bằng một ma trận khuếch tán : các thành tố của ma trận là những biên độ (số phức) chuyển tiếp, và bình phương môđun của chúng cho ta xác suất của các sự kiện xuất hiện trong chuyển tiếp.
Điều cần ghi nhớ đằng sau tất cả những dạng thức toán học này, là một bước tiến tới nữa trong quá trình loại bỏ dần khái niệm thực thể để nhường chỗ cho khái niệm trường, đã được Einstein và Infeld nêu lên khi nói về điện động học (xem chương 3). Trường không còn đơn giản là một thủ thuật toán học nữa, nó trở thành một khái niệm tiên khởi của vật lý vi hạt : vi hạt - khối lượng / vi hạt - năng lượng của thuyết tương đối đã bị lu mờ sau quantum tác dụng(iv) của cơ học lượng tử, và đến lượt nó khái niệm này lại tự xoá mờ để hiện hình ra thành một quantum tương tác giữa các trường lượng tử.
Để diễn tả rõ hơn quan điểm trên, chúng ta hãy theo quy ước trong [CTS] để viết hoa khi nói về các trường, và viết chữ thường khi nói về lượng tử (photon là lượng tử của trường Photon; trường Điện tử có hai lượng tử là điện tử âm và điện tử dương) bây giờ ta lấy thí dụ về điện động học lượng tử (QED) : « Trên quan điểm vi hạt, QED là lý thuyết về sự tương tác giữa các điện tử âm và dương, và photons ; trên quan điểm trường lượng tử, đó là lý thuyết truyền bá và ghép đôi của Điện tử và Photon » ([CTS] tr.192). Về cuối đời (sau công trình lượng tử hoá lần thứ hai của Dirac, nhưng trước khi có bùng nổ của các lý thuyết QFT ), Planck đã nói, có phần thản nhiên cam chịu : « Tôi vốn là người đã dành cả cuộc đời cho bộ môn khoa học chặt chẽ nhất, nghiên cứu về vật chất, sau đây là tất cả những gì tôi có thể nói với bạn về những kết quả nghiên cứu của tôi : không có vật chất đâu ! » (1947)
6- Từ đối xứng chuẩn tới mô hình chuẩn
Trong cơ học phân tích cũng như trong lý thuyết trường, người ta sử dụng một số nhỏ những nguyên lý cơ bản về « đối xứng » để xây dựng hàm Lagrange, và từ đó suy ra những bất biến động, có nghĩa những đại lượng không đổi trong khi hệ thống đang vận động. Trong QFT, chính sự biểu diễn những bất biến này như là hàm của các toán tử liên hợp diệt và sinh đưa đến các hệ thức giao hoán đặc trưng của trường (xem chương 5). Không nên hiểu thuật ngữ không rõ rệt « đối xứng » theo một nghĩa toán học chật hẹp (đối xứng qua điểm, hay trục...), mà nên cho nó một nội dung trực giác rộng rãi hơn : Nếu suy xét kỹ chúng ta sẽ thấy rằng các quy luật vật lý đã trình diện trong bài này đều được đặt trên nền tảng của một vài nguyên lý bảo tồn đơn giản đến mức đáng ngạc nhiên, chẳng hạn như sự bảo tồn khối lượng / năng lượng, xung lượng, mômen xung lượng(v)... Nhưng chúng ta cũng đã thấy, tính chất thực dụng của các nguyên lý này hiển lộ ngay khi người ta tìm cách định nghĩa một cách thực rõ rệt cái đại lượng được bảo tồn. Trên thực tế, việc toán học hoá những khái niệm này chỉ mới có từ những nằm đầu thế kỷ 20, theo dòng phát triển của chương trình nghiên cứu toán học Erlangen, với định lý của Emmy Noether, rồi đến những đối xứng chuẩn của Hermann Weyl.
Emmy Noether (1882-1935) (1)
Chương trình Erlangen lừng danh do David Hilbert và Félix Klein đề nghị năm 1872 nhằm đặt nền tảng toán học cho hình học trên những tác động nhóm và những cái bất biến trong các tác động đó. Xin nhắc lại nhanh, một nhóm là một tập hợp các toán tử mang theo một luật hợp thành * , luật đó tuân thủ một số quy tắc như tính kết hợp (tức a*(b*c) = (a*b)*c), nhưng không giao hoán (tức a*b không cần phải bằng b*a). Nếu tập hợp E, trên đó nhóm G thao tác, bản thân nó cũng mang một cấu trúc (không gian vectơ, không gian Hilbert, xem chương 4), và nếu G bảo tồn cấu trúc ấy, ta định nghĩa G là một nhóm đối xứng đối với cấu trúc của E.
Một thí dụ tiêu biểu về nhóm và những bất biến của nó là nhóm Lorentz trong thuyết tương đối hẹp. Sau đây là một thí dụ khác, sơ đẳng nhưng đáng giá ở chỗ nó cho phép phân biệt giữa các biến đổi « rời rạc » và biến đổi « vô cùng nhỏ » : cho E, tập hợp các điểm trên một mặt phẳng được quy chiếu bằng một điểm gốc O ; và cho G, nhóm các phép quay chung quanh O theo nghĩa quen thuộc ; E có thêm một cấu trúc là « Mêtric euclid », cấu trúc này cho phép đo khoảng cách giữa hai điểm ; hiển nhiên, bởi vì G thao tác trên E và bảo tồn mêtric đó, G là một nhóm đối xứng đối với E theo nghĩa nói trên, mà ký hiệu là SO(2,R) (hai kích thước thực) hoặc U(1,C) (một kích thước phức). Về thí dụ cho những bất biến, ta hãy xem một vòng tròn và một hình vuông, cả hai đều lấy tâm điểm là O. Mỗi phép quay bằng bất cứ trị số góc nào, dù nhỏ đến đâu (người ta gọi như thế là vô cùng nhỏ) đều bảo tồn hình dạng chung của vòng tròn ; về thực chất, tập hợp những phép quay đó chính là bản thân nhóm G. Trong khi đó, chỉ có những phép quay với một góc bằng 90 độ hay bằng một bội số của nó mới bảo tồn hình dạng chung của hình vuông ; những phép quay rời rạc đó hợp thành một nhóm con của G có 4 phần tử.
Trong tinh thần chương trình Erlangen, một sinh viên của Hilbert và Klein, Emmy Noether (mà tên tuổi sẽ được gắn liền chủ yếu với những công trình quan trọng về đại số giao hoán của bà) đã chứng minh được vào năm 1903 một định lý về những bất biến vi phân trong phép tính biến phân, mà hiện nay được coi như « một trong những định lý toán học đã chứng tỏ là quan trọng nhất trong việc định hướng phát triển cho vật lý học từ xưa tới nay » (Leon Lederman, giải Nobel 1988), bởi vì nó thiết lập một quan hệ chặt chẽ, trong sự vận động của một hệ thống, giữa tính bảo tồn (của một đại lượng vật lý) và tính bất biến trong đối xứng (của một tính chất vật lý) : « Với bất cứ một biến đổi vô cùng nhỏ nào mà tích phân của tác dụng được giữ nguyên, đều có một đại lượng vật lý tương ứng được bảo tồn ». Nghịch đảo lôgic của định lý Noether đưa đến một ý tưởng khai phá cực kỳ quan trọng : nếu một đại lượng vật lý được bảo tồn, thì những quy luật (mà ta phải khám phá) điều khiển hoạt động của nó phải bất biến đối với một sự biến đổi nào đó có tính đối xứng liên tục ; nếu người ta nắm bắt được một đối xứng như thế, hay hơn nữa, được cả một nhóm đối xứng, thì khi đó người ta loại bỏ được rất nhiều mảng cấu trúc toán học không có khả năng, mà còn có thể tìm cách xác định những liên hệ tiềm ẩn giữa các quy luật điều khiển những đại lượng vật lý có liên quan đến nhóm đối xứng đó. Đó là, nói một cách sơ sài, phương pháp tiến hành trong các lý thuyết trường chuẩn.
Hermann Weyl (1885-1955)
Đã đến lúc chúng ta cần định nghĩa thế nào là một đối xứng chuẩn định xứ (vi), một khái niệm được đưa ra (nhưng với cái tên không đẹp cho lắm) bởi nhà toán học Đức Hermann Weyl, năm 1918. Tuy rằng ông được biết đến chủ yếu vì những công trình quan trọng về lý thuyết các nhóm biến đổi liên tục có tên « các nhóm Lie », Weyl cũng để tâm đến vật lý lý thuyết và cộng tác với Einstein.
Ý tưởng khởi đầu của Weyl như sau : các quy luật bảo toàn phải được liên kết, không phải với một nhóm đối xứng duy nhất cho tổng thể, mà với một trường các nhóm định xứ, mỗi nhóm tác động trên một điểm của không thời gian, và là một phiên bản của một nhóm gọi là nhóm đối xứng chuẩn. Để nói rõ hơn một chút, ta hãy xem hàm số sóng \(|\psi\rangle = |\psi(\mathbf{r},t)\rangle\), trong đó r là vectơ định vị không gian và t là thời gian. Hàm Schrödinger xác định biến thiên của \(|\psi\rangle\) rõ ràng là bất biến trong một chuyển pha tổng quát, có nghĩa trong biến đổi do phép nhân \(|\psi\rangle\) với một số phức có môđun bằng 1 (mà pha của nó là « toạ độ góc » theo ngôn ngữ toán), độc lập với vectơ bốn chiều (r,t) : đó là một bất biến của đối xứng chuẩn tổng quát với nhóm U(1). Nhưng nếu sự chuyển pha phụ thuộc vào (r,t), như trong mọi trường theo đúng nghĩa, hàm Schrödinger không còn bất biến nữa. Nếu chúng ta cá biệt hoá \(|\psi\rangle\) khi coi hàm sóng Maxwell cổ điển, thì bất biến của đối xứng chuẩn có định xứ với nhóm U(1), xác định theo Weyl, được suy ra bằng cách làm xuất hiện một tương tác giữa những trường lực kết nối với thế-vectơ và với điện thế. Tình huống này được giữ nguyên khi chuyển qua khung cảnh QFT, bằng cách thay những thế cổ điển bằng các trường Photon và Điện tử. Các bosons hiện ra trong một tương tác như vậy – ở đây là photon – được gọi là các bosons chuẩn.
Ước vọng của Weyl thời ấy là thống nhất điện động học và thuyết tương đối rộng, bằng cách gán cho bản thân không gian một bất biến chuẩn. Ý tưởng ấy không thực hiện được với trường hấp dẫn, nhưng chính nó đã đứng đằng sau những lý thuyết trường chuẩn liên tiếp thành công trong việc soi sáng các tương tác mạnh và yếu, ngay cả đằng sau việc thống nhất tương tác điện từ với tương tác yếu. Công cuộc tổng hợp này đã hình thành « mô hình chuẩn » vĩ đại, thống nhất được tất cả các tương tác cơ bản, ngoại trừ trường hấp dẫn (thuộc phạm vi của thuyết tương đối tổng quát).
Các lý thuyết trường chuẩn
Dưới đây chúng tôi dùng một bảng để tóm tắt các lý thuyết trường chuẩn khác nhau cuối cùng đã hợp thành mô hình chuẩn, cùng với các nhóm đối xứng chuẩn liên kết với từng lý thuyết. Một sự kiện đáng để ý, các lý thuyết này không tiến triển một cách riêng lẻ, mà có liên lạc chặt chẽ với nhau, sử dụng kết quả của nhau, quá trình này cần đến nhiều năm cố gắng kiên trì cho từng lý thuyết trên những con đường đôi khi song hành, đôi khi đan chéo (xem [B]). Chúng đã mang đến cả một mùa gặt hái giải Nobel, nhưng quan trọng nhất là chúng còn minh chứng, hơn bao giờ hết, câu nói của Newton : « Nếu tôi đã có thể nhìn xa như thế, chính là vì tôi đứng trên vai những người khổng lồ đã đi trước ».
| Điện động học lượng tử QED | Nhóm U(1) | Lực điện từ |
| Thuyết thống nhất điện yếu | SU(2)xU(1) | Lực điện từ và lực yếu |
| Sắc động lực học lượng tử QCD | SU(3) | Lực mạnh |
| Mô hình chuẩn | SU(3)xSU(2)xU(1) | Thống nhất ba lực |
Ta còn cần thêm một số giải thích tối thiểu. Trước hết về các nhóm : mọi số hạng đều là số phức, người ta ngầm hiểu về ký hiệu C đã nói đến từ trước ; khi đó U(n) chỉ định nhóm các toán tử (được gọi là đơn nguyên) có đặc tính bảo tồn cấu trúc của một không gian Hilbert có chiều kích hữu hạn bằng n, và SU(n) là nhóm con gồm những toán tử đơn nguyên có định thức bằng một. Ngay cả một người bình thường cũng biết đến U(1), đó là nhóm các pha, tức các góc được định nghĩa trong vòng 360 độ, thêm hay bới 2π vẫn thế (hay gọi là modulo 2π theo ngôn ngữ toán). Trong tất cả các U(n), chỉ có U(1) là nhóm giao hoán (còn gọi là nhóm abel).
Sau nữa, về các tương tác : Chúng ta đã thấy rằng U(1) hiện ra như một nhóm đối xứng chuẩn tự nhiên của điện động học cổ điển. Vậy còn phải chuyển sang đối tượng tương ứng với điện động học lượng tử QED (để ý là QED cũng hay được dùng trong toán học để viết tắt thành ngữ la-tinh quod erat demonstrandum, đó là điều phải chứng minh, dân khoa học thường ham thích kiểu chơi chữ này), nhưng việc lượng tử hoá trường điện từ thời ấy đã gặp phải những khó khăn không khắc phục được, ngay cả với Einstein, ông đã chịu thua qua câu pha trò : « Hình như Thượng Đế có một ngón nghề » (1910). Ngón nghề, chính là làm sao mở rộng việc áp dụng cho các trường lượng tử khái niệm tích phân tác dụng – nói kiểu giáo khoa, đó là tích phân của hàm Lagrange trên không gian cấu hình – để có thể áp dụng một nguyên lý tác dụng tối thiểu, như trong cơ học phân tích và quang học ba động. Điều này đã được Feynman viết trong một bài báo năm 1948, trong đó ông đưa ra khái niệm tích phân lộ trình (đừng nhầm với tích phân đường cong trong cơ học cổ điển) :
Ông từ bỏ việc tính toán xác suất cho hiện tượng một vi hạt xuất hiện ở một điểm nào đó trong không thời gian, mà sử dụng xác suất để nó đi theo một quỹ đạo (một « lộ trình », hay một « vũ trụ tuyến ») nằm trong một vùng nào đó của không thời gian ; cùng lúc đó giả định rằng phần của mỗi lộ trình có thể có bằng hàm số mũ của i lần tác dụng cổ điển (theo định nghĩa đó là một con số « thuần pha »), sau đó ông chứng minh là tổng của các xác suất của tất cả các lộ trình đi từ quá khứ đến điểm (r,t) chính là hàm số sóng \(|\psi(\mathbf{r},t)\rangle\) thoả mãn phương trình Schrödinger ([CTS], tr.187).
Phải nói ngay rằng cái « ngón nghề » của Feynman, mặc dù nó quá đẹp nên không thể không đúng, cũng không tự nhiên được bảo đảm bằng toán học :
trong tích phân lộ trình của Feynman, biến số của tích phân không còn nằm trong không gian bình thường của lý thuyết tích phân, mà nằm trong một không gian các hàm, không cùng độ đo, từ đó xuất hiện vấn đề « phân kỳ », tức là tích phân có thể trở thành vô tận ! Để tiếp cận vấn đề, trên thực tế người ta dùng một « phép khai triển nhiễu loạn », tức là một phép khai triển thành chuỗi, dựa trên các luỹ thừa của hằng số ghép đôi giữa các trường tương tác với nhau, mà các hệ số chỉ liên quan đến các tích phân theo nghĩa thông thường. Các biểu đồ của Feynman cung cấp nhiều cách thức để tính toán những hệ số đó, nhưng trong một số trường hợp, khi mà biểu đồ có « vòng khép », tích phân lộ trình thực sự là phân kỳ.
Cách cứu chữa chủ yếu là dùng một phương thức rất chuyên môn có tên tái chuẩn hoá (Feynman, Schwinger, Tomonoga, giải Nobel 1965), mà ở đây không cần đi vào chi tiết, ngoài nhận xét là tình hình không phải lúc nào cũng khả quan : cần thiết phải xem xét từng trường hợp một, với mỗi lý thuyết trường chuẩn phải chứng minh là nó có thể được tái chuẩn hoá. Cho đến năm 1972, ‘t Hooft và Veltman (giải Nobel 1999) chứng minh được là tất cả những lý thuyết trường chuẩn kiểu Yang-Mills với « phá vỡ đối xứng » (xem phía dưới) đều có thể được tái chuẩn hoá.
Sự thành công của QED, một lý thuyểt đã có thể tiên đoán các kết quả thí nghiệm với độ chính xác kinh hoàng (về « hệ số Lander » của điện tử, độ chính xác đạt được là tương đương với bề ngang một sợi tóc chia cho khoảng cách từ Los Angeles tới NewYork !), chỉ có thể kích thích các nhà nghiên cứu đi tìm những lý thuyết trường chuẩn tương tự, nhưng không abel (có nghĩa được kết hợp với các nhóm đối xứng chuẩn không giao hoán).
Thuyết của Yang và Mills, thiết lập vào khoảng đầu những năm 1950 để giải thích tương tác mạnh, thực ra có thể được áp dụng cho tất cả các nhóm Lie compac nửa-đơn-giản, chính vì thế người ta hay dùng số nhiều khi nói về nó. Ở điểm khởi đầu, Heisenberg đã phát biểu giả thuyết là proton và nơtron kết hợp với nhau trong lõi nguyên tử bằng cách trao đổi một điện tử, và đưa ra khái niệm isospin (tương tự như spin, nhưng chi là tương tự thôi) để phân biệt hai trạng thái của vi hạt nơtron/proton. Yang và Mills nhận dạng isospin như một đối xứng chuẩn có định xứ, theo kiểu đối xứng U(1) trong QED, nhưng, vì ở đây có hai vi hạt làm đối tượng, cần phải mở rộng nhóm đối xứng chuẩn. Khi đã chọn SU(2), hậu quả là họ phải đưa vào một trường mới, đặt tên là B, kèm theo ba vi hạt chuẩn, đặt tên là B+ (cho tương tác proton-nơtron), B- (cho tương tác ngược lại) và B° ( cho tương tác nơtron-nơtron). Đọc đến đây bạn đọc chắc đã nhận ra vai trò của hai toán tử sinh/diệt. Nhưng, mô hình này không thành công, một mặt vì nó không tái chuẩn hoá được, mặt khác vì số hạng zêrô của khai triển nhiễu loạn chỉ ra là khối lượng của những vi hạt trung gian có trị bằng không, do đó tầm ảnh hưởng của tương tác là vô tận (xem chương 5, đoạn về khối lượng của meson), mâu thuẫn toàn bộ với tương tác mạnh (2).
Nhưng hướng nghiên cứu của Yang và Mills vẫn có giá trị, với điều kiện là phải thay đổi nhóm đối xứng chuẩn. Bài toán sẽ được thuyết sắc động học lượng tử, QCD, giải quyết ; QCD do Gross, Politzer và Wilczek (giải Nobel 2004) đề xuất, đó là một lý thuyết trường chuẩn SU(3) : tương tác mạnh là do sự trao đổi sắc giữa các quarks, thông qua vi hạt gluons.
Để tránh lại phải nghe lời tán thán « quái quái đản đản ! », chúng tôi vội vàng xin thưa là các hạt quarks – tên do Gell-Mann (giải Nobel 1969) sáng chế, và đó là trò chơi chữ rút ra từ truyện «Finnegan’s Wake» của J. Joyce – là các thành phần cơ bản nhất của những hadrons ; các gluons là những vi hạt của trường chuẩn SU(3), các bosons không khối lượng, có tám (= kích thước của nhóm Lie SU(3)) ; Ba sắc (xanh, đỏ, xanh lá cây) là những số lượng tử (xem chương 5), tổ hợp thành sắc tích, được gọi như thế do tương tự với điện tích của thuyết điện-yếu ; các hạt « mang sắc tích » tương tác với nhau bằng cách trao đổi sắc, sắc tích trắng, tổ hợp của ba sắc kia, là cái duy nhất trung lập ; vấn đề tầm tương tác liên quan đến khối lượng zêrô bị loại bỏ bởi bản chất đặc biệt của lực hút giữa các sắc, nó tăng theo khoảng cách, và giam chặt quarks bên trong các hadrons. Loạt bài này có ý định tập trung trên boson BEH, vì thế chúng tôi không quyến luyến với tương tác mạnh nữa mà xin chuyển sang nói về tương tác yếu.
Vào khoảng cuối những năm 1950, sự tương tự (chỉ tương tự thôi) giữa giả thuyết của Heisenberg và phản ứng phân rã bêta (xem đoạn đầu chương 5) đã khiến Schwinger (giải Nobel 1965 cùng với Feynman và Tomonoga, xem bên trên) và sinh viên tên Glashow của ông, độc lập với Yang và Mills, đưa vào ba vi hạt, ba bosons của isospin yếu W+, W- và Z° (theo thuật ngữ hiện nay) để giải thích tương tác yếu. Sự hiện diện của điện tích gợi ra ý tưởng là trước hết cần thiết phải xây dựng một lý thuyết hợp nhất được lực tương tác yếu và lực điện từ, điều mà ngày nay được gọi là lý thuyết điện yếu. Glashow chọn lựa nhóm đối xứng chuẩn SU(2)xU(1), nhưng rồi gặp phải cùng một chướng ngại như Yang và Mills, đó là mô hình này không tái chuẩn hoá được, với những vi hạt trung gian có khối lượng bằng không. Làm thế nào đem lại cho các vi hạt này một khối lượng ? Giải pháp sẽ đến là phải sử dụng khái niệm phá vỡ đối xứng tự phát của Nambu (giải Nobel 2008) và Goldstone, bổ sung bằng cơ chế BEHGHK mà chúng ta sẽ nói đến sau. Áp dụng vào lý thuyết đối xứng chuẩn SU(2)xU(1) của Glashow, cơ chế này cho phép Abdus Salam và Steven Weinberg, độc lập với nhau, cùng hoàn thành năm 1967 lý thuyết thống nhất điện yếu cho các leptons : « phóng chiếu » xuống nhóm U(1), lý thuyết này tìm lại được QED, sự phá vỡ đối xứng cho phép gán khối lượng cho các bosons W+, W- et Z° (vào khoảng 85 lần khối lượng proton cho W, 96 lần cho Z), và thêm nữa, nó còn tiên đoán một vi hạt vật chất thứ tư, boson BEH. Bộ ba Glashow-Salam-Weinberg được giải thưởng Nobel năm 1979, khá lâu trước khi ba bosons nói trên được làm hiện rõ trong máy gia tốc LEP của CERN năm 1983. Còn hạt cuối cùng kia ? chính sự phát hiện ra nó trong LHC đang là vấn đề thời sự.
Khi boson xuất hiện…
Sự phá vỡ đối xứng tự phát của một hệ thống là hiện tượng thường xẩy ra trong cơ học thống kê, được kích hoạt khi có đối nghịch giữa tính ổn định của một trạng thái cơ bản (trạng thái năng lượng cực tiểu) với tính đối xứng trong vận động của hệ thống, dưới ảnh hưởng của các dao động thăng giáng không chế ngự được (nhiệt, lượng tử) và không mang tính đối xứng nói trên. Để thí dụ ta hãy tưởng tượng một hòn bi đặt cân bằng trên chỏm một cái mũ Mễ Tây Cơ (hình 6.1), mà dạng đối xứng tổng quát là hình tròn : đỉnh mũ ở trạng thái năng lượng cực trị, nhưng không ổn định ; cái rãnh theo vành mũ cũng ở trạng thái năng lượng cực trị, nhưng ổn định ; một dao động thăng giáng (mặt trời, gió, rung động) có thể làm phá vỡ sự thăng bằng và làm cho hòn bi rơi xuống rãnh mà không tốn năng lượng : đó là sự phá vỡ đối xứng tự phát.
Trong các lý thuyết lượng tử, chân không là một trạng thái cơ bản, trạng thái năng lượng cực tiểu. Khi có thể có nhiều trạng thái chân không, một số thì ổn định nhưng không đối xứng định xứ, một số khác thì không ổn định nhưng lại có đối xứng tổng quát, người ta có thể « đổi trạng thái chân không » mà không tốn năng lượng ; nhưng nguyên lý Nambu-Goldstone (1956) đã xác định là một thay đổi như thế phải làm xuất hiện một lượng tử của một trường vật chất, cũng là một vi hạt có cùng số lượng tử với chân không, trung hoà, có spin bằng không, không khối lượng, boson của Nambu-Goldstone. Khi đối xứng phá vỡ tự phát là một đối xứng chuẩn định xứ abel (thành phần U(1) của nhóm chuẩn SU(2)xU(1)), việc chuyển từ một chân không đối xứng sang một chân không bất đối xứng phải tương ứng với một thay đổi chuẩn. Khi đó boson của Nambu-Godstone sẽ ra sao ? Để cho đối xứng chuẩn U(1) của QED được bảo tồn, thì bất biến của chuẩn định xứ (xem đoạn đầu chương này) cần tương tác với một trường khác, trường BEH. Đó là sự kích hoạt cơ chế BEH, các lượng tử của trường BEH tổ hợp với các bosons không khối lượng của Nambu-Godstone để phát sinh một photon và bốn bosons có khối lượng, W+, W- et Z° và BEH.
Bản tổng kết, dù sao cũng khá phức tạp, được vẽ thành biểu đồ trong hình 6.2. Lưu ý là, trong nghiên cứu của mình về sự phá vỡ đối xứng, Nambu cũng đã có trực giác về một trường thuộc loại « phép mầu được dàn cảnh ». « Chuyện gì sẽ xẩy ra nếu một loại vật liệu siêu dẫn nào đó tràn ngập vũ trụ trong đó chúng ta sống ? Bởi vì chúng ta không thể quan sát cái thực sự là chân không, trạng thái cơ bản của môi trường nói trên sẽ trở thành, trên thực tế, chân không. Nhưng như thế thì, ngay cả những vi hạt giả thử là không có khối lượng […] trong chân không thực sự, sẽ có được khối lượng trong thế giới hiện thực ». Điều ấy chỉ là tư biện (3), nhưng dù sao thì, các bài báo đầu tiên của Brout-Englert và của Higgs (1964) mỗi bài chỉ dài... có một trang rưỡi thôi !
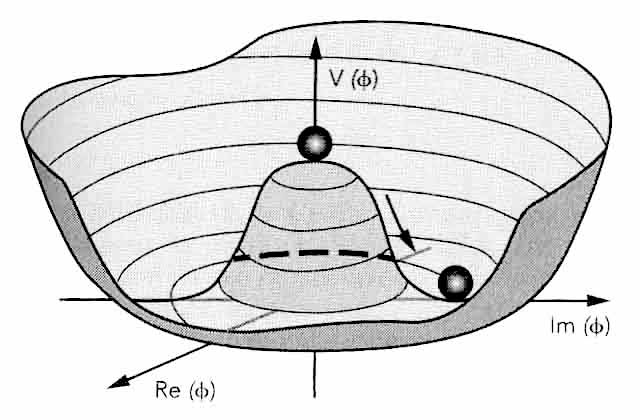
Hình 6.1 Thế tương tác tự phát của trường BEH dưới dạng mũ Mễ Tây Cơ
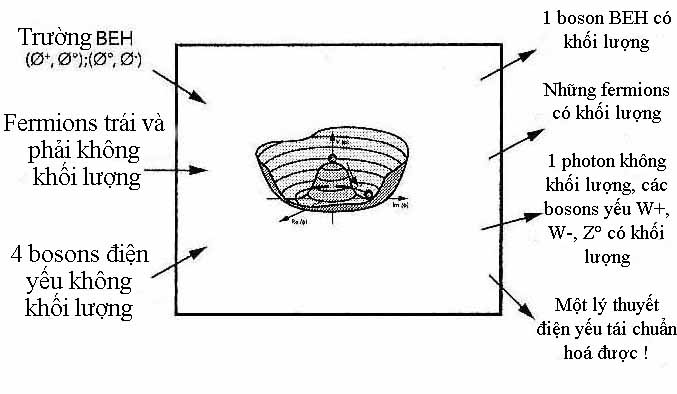
Hình 6.2 Biểu đồ tổng kết cơ chế BEH
Để mời bạn đọc món tráng miệng cho đầy đủ, chúng ta có thể mô tả cơ chế BEH theo kiểu ví von, giống như nhà vật lý David Miller đã làm năm 1990 (dẫn trong [B]) để kiếm sự ủng hộ dự án LHC của CERN từ các nhà chính trị Anh quốc thời ấy. Miller thì đưa bà Thatcher lên sân khấu, nhưng thay vì thế chúng ta có thể tưởng tượng bữa tiệc tiếp tân nhân dịp trao các giải Nobel, với việc các khách mời chiếm chỗ một cách đồng đều trong phòng tiệc. Bây giờ là lúc các « giải nguyên » tiến vào, đi đầu là Higgs ; ông tìm cách mở ra một con đường để tiến tới trong cái « trường » đó, các khách mời thì lại tụ tập chung quanh họ, càng làm cho bước đi của đoàn chậm lại : tương tự như việc một boson không khối lượng trở thành có khối lượng. Cùng lúc ấy, tin đồn các giải nguyên đã đến được truyền đi trong phòng, làm cho các khách mời tụ lại với nhau bàn tán : đó là boson BEH được sinh ra trong « trường ».
Như vậy là chúng ta đã đến giai đoạn cuối của cuộc xây dựng lý thuyết điện yếu, trong đó boson BEH chiếm vị trí của khối đá chốt vòm. Người ta thấy trong biểu đồ tương tác của hình 6.3 là boson BEH cũng đem lại khối lượng cho quarks, và do đó uỷ ban Nobel đã có lý khi bình luận rằng « nếu không [có boson đó] đã không có chúng ta ».
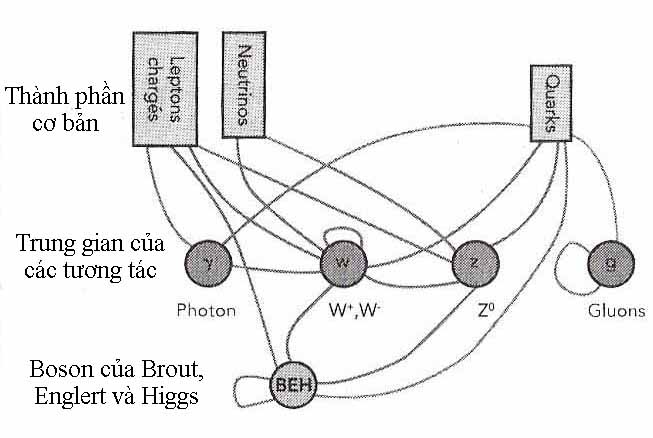
Hình
6.3 các tương
tác trong mô hình chuẩn điện
yếu.
Các vi hạt trực tiếp tương
tác với boson BEH trở nên
có khối
lượng. Nhưng các neutrino cũng có
khối lượng.
Nhưng phải chăng đó đã là chìa khoá cuối cùng, « vi hạt của thượng đế » ? Không hẳn thế, mô hình chuẩn, tức lý thuyết chuẩn U(1)xSU(2)xSU(3) bao trùm tất cả các lý thuyết chuẩn khác, còn chưa đạt đến độ chín muồi trọn vẹn : nó còn chứa quá nhiều độ tự do (19), ngược lại với nguyên lý tiết kiệm (hay « dao cạo của Occam ») ; những hiện tượng như là khối lượng của neutrino còn chưa được giải thích : Sự « cầm giữ » các quarks còn đợi một mô hình toán học (và đó cũng là một trong 7 bài toán của thiên niên kỷ với giải thưởng 1 triệu đôla của viện Clay cho mỗi bài) ; và nhất là, tương tác hấp dẫn (thuyết tương đối tổng quát) còn nằm ngoài mô hình chuẩn. Chưa nói đến những vấn đề của vũ trụ học, người ta đang chờ đợi một cuộc tổng hợp cuối cùng, một « lý thuyết cho mọi thứ » (GUT, grand unified theory) sẽ giải thích được... mọi thứ. Trong khi chờ đợi, và ở thời buổi mà chủ nghĩa thương mại hoá tự cho mình là chân trời không thể vượt qua của xã hội loài người, thực ấm lòng khi thấy biết bao nhiêu tài năng, có khi là thiên tài, vẫn tiến bước, đơn lẻ hay tập thể, trên con đường gian nan của hiểu biết.
Nguyễn Quang
Bản dịch: Hàn Thuỷ
Nguồn hình ảnh : Tất cả các hình ảnh minh hoạ đều chép từ bách khoa toàn thư mở Wikipedia, trừ những hình 6.1, 6.2 và 6.3 chụp lại (và dịch sang việt ngữ) từ chương 7 của [CTS].
(1) Einstein đã chào đón Emmy Noether như là « thiên tài sáng tạo toán học lớn nhất mà giáo dục đại học phụ nữ đã đào tạo ra ». Nhưng, mặc dù danh tiếng như thế, bà không bao giờ được bổ nhiệm một chức vụ đại học nào cao hơn là Privatdozen (trợ giáo). Trách nhiệm của sai lầm này dĩ nhiên thuộc về sự kỳ thị giới tính đương thời. Năm 1900, Emmy Noether là một trong hai nữ sinh viên duy nhất được nhận vào đại học Erlangen. Năm 1915, khi Hilbert tìm cách bổ nhiệm bà vào đại học Göttingen, ông đụng phải những đối kháng kiểu như : « Quân sĩ của chúng ta sẽ nói gì khi mà trở lại đại học, họ sẽ phải chịu cái ách của một người đàn bà ? » Phản pháo của Hilbert : « Đây là đại học, không phải nhà tắm công cộng ! »
(2) Nghe đồn rằng khi Yang trình bày thuyết của mình năm 1954 trong một xêmina « súng săn » ở Princeton, có tên này vì các thuyết trình viên ở đó bị « tàn sát » nhiều hơn thường lệ. Điều không tránh khỏi, vì Pauli đã truy vấn Yang tới cùng về khối lượng của trường B lẫy lừng này. Đến nỗi mà Oppenheimer phải can thiệp để Yang khốn khổ có thể tiếp tục thuyết trình.
(3) Có vẻ như ête lại xuất hiện, nhưng đây chỉ là một sự tương tự.
(i) RQM = Relativistic quantum mechanics = Cơ học lượng tử tương đối tính ; QFT = Quantum field theory = lý thuyết trường lượng tử. Người dịch (n.d.) đề nghị giữ nguyên cách viết tắt đã phổ biến trên thế giới.
(ii) n.d. : những thuật ngữ này hoàn toàn không liên hệ với ý nghĩa bình thường của chúng, chúng chỉ được đặt ra cho dễ nhớ, thực ra dịch hay không dịch cũng vậy.
(iii) dịch chữ superposition trong trường hợp « chập trùng » của nhiều hơn hai trường, nếu hàm ý hai, trong chương 4 đã dịch là « song trùng »
(iv) trong bài này thuật ngữ « action » được dịch tuỳ văn cảnh là « tác động » theo thuật ngữ toán học (biểu thị một « hành động » gần với nghĩa trực giác thông thường, ở đây là một phép biến đổi từ đầu vào sang đầu ra), và « tác dụng » theo thuật ngữ vật lý (biểu thị kết quả của một tiến trình, điều có thể đo lường được, và cũng là theo định nghĩa chung của vật lý học).
(v) thuật ngữ « moment cinétique » có những cách dịch sau đây : xung lượng góc, động lượng góc, xung lượng quay, động lượng quay, mômen xung lượng, mômen động lượng... cũng tương tự « impulsion » ngày trước đã được dịch là xung lượng, ngày nay, với phần lớn các quy chiếu trên mạng, đó là động lượng. Trong phần trước của bài chúng tôi đã xử dụng thuật ngữ phần nào đã cũ trong « Từ điển vật lý Anh Việt » (nxb Khoa Học và Kỹ thuật, HàNội, 1976) là mômen xung lượng, xin tạm giữ nguyên trong khi chờ đợi một từ điển thuật ngữ vật lý có hệ thống, thống nhất và đầy đủ.
(vi) dịch theo Gs Phạm Xuân Yêm, Mô hình Chuẩn của Vật lý Hạt cơ bản, Tia sáng 10/10/2013
Các thao tác trên Tài liệu










