Vài ngộ nhận về
ALBERT EINSTEIN

NGUYỄN XUÂN XANH

Có nhiều ngộ nhận về Albert Einstein. Trên mạng, nhiều sự gán ghép, nhái giọng văn ông, và được lan truyền mà không ai biết rõ nguồn gốc, như thể do chính Einstein nói. Vào các quán chay Việt Nam, người ta thấy trong danh sách các danh nhân ăn chay trường có cả Einstein. Hoặc Einstein là người thuận tay trái. Những chuyện đó không đúng sự thật. Einstein chỉ ăn kiêng theo yêu cầu của bác sĩ trong những lúc ông bệnh cần kiêng cữ, chứ không ăn chay trường, không có quyển sách nào viết về điều đó, cũng như viết về sự thuận tay trái của Einstein cả. Ngược lại có những tấm ảnh tư liệu cho thấy Einstein cầm bút tay phải, như một minh họa dưới đây.

Nhưng trong bài này, có hai sự ngộ nhận lớn mà chúng tôi muốn đề cập đến, một liên quan đến khoa học, về nghi vấn Hilbert là người đến đích trước, hay cùng lúc với Einstein, trong cuộc chạy đua thiết lập các phương trình trường của thuyết tương đối rộng vào năm 1915. Và thứ hai, liên quan đến tôn giáo, đến một phát biểu “rất Einstein” về Phật giáo từ lâu được lưu truyền và cho là của Einstein. Thiết tưởng đã đến lúc chúng ta cần làm sáng tỏ.

(1) 

Tranh cãi quyền ưu tiên về Thuyết tương đối rộng
giữa Einstein và Hilbert

Hiếm có người nào hiểu lý thuyết này (tương đối rộng) lại có thể thoát khỏi ma lực của nó.

Albert Einstein

Các phương trình trường (field equations) của Einstein là cao điểm, và cốt lõi của Thuyết tương đối rộng mà Einstein đã miệt mài đi tìm từ 1907-1915. Chúng không được suy ra dễ dàng theo lô gíc từ những nguyên lý của ông. Con đường đi tìm đầy gập ghềnh xen lẫn ảo giác. Đó là kết hợp của toán học và trực giác vật lý. Einstein bắt đầu thuyết này lúc 28 tuổi, khi còn là “chuyên gia” đơn thuần ở Sở Sáng chế Bern, và kết thúc ở Berlin 8 năm sau, lúc ông 36 tuổi, khi ông là giáo sư và thành viên của Hàn lâm viện khoa học Phổ.

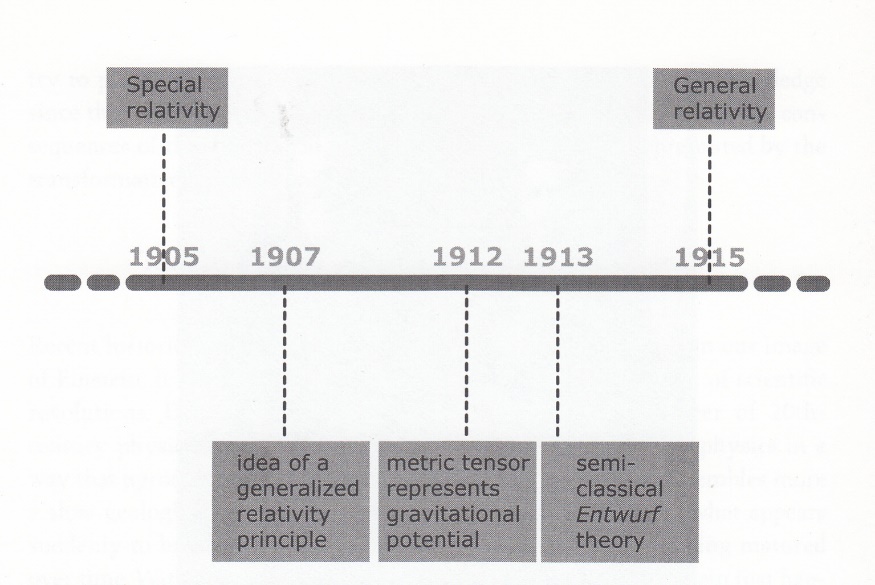
(Thuyết Tương đối, từ Hẹp tới Rộng, theo Jürgen Renn [3])

Dĩ nhiên, ai tìm ra được các phương trình này có thể được xem là cha đẻ của toàn bộ học thuyết. Một thời gian dài sau khi Einstein công bố thuyết của ông, có nhiều người tin hay muốn tin rằng, vào những giây phút cuối Einstein đã bị ‘vấp ngã’, và cho phép Hilbert, một trong những nhà toán học vĩ đại bấy giờ, qua mặt ông. Hoặc: thật sự ai là cha đẻ của phương trình trường, Einstein, hay Hilbert, hay cả hai?

Thực sự, Einstein đã từng công bố (1913), chung với bạn ông, Marcel Großmann, Entwurf (Phác thảo) của thuyết tương đối rộng. Ở đó các phương trình trường đã có, nhưng vì một suy luận (Suy luận lỗ trống, hole argument, liên quan đến khoảng không giữa các khối vật chất), nên ông đã từ bỏ nguyên lý hiệp biến chung (general covariant principle). Năm 1915, ông nhận ra rằng đó là sai lầm.

Tờ 20L của Sổ tay ghi chép Zurich (trong [3])

Theo cái nhìn hình thức, David Hilbert đã hoàn tất thuyết tương đối rộng ít nhất 5 ngày trước báo cáo kết thúc của Einstein vào ngày 25 tháng 11 chứa đựng các phương trình trường cuối cùng của thuyết tương đối rộng. Bài báo của Hilbert, đề ngày 20 tháng 11, nhưng xuất bản ngày 31 tháng 3, 1916, trình bày một thuyết hấp dẫn hiệp biến tổng quát, và cả các phương trình trường tương đương với các phương trình trong bài báo của Einstein. Vì lý do đó, nhiều người nghĩ rằng ít nhất Hilbert cũng phải “có phần” trong thuyết tương đối rộng. Hay có người nghi ngờ Einstein đã “cóp” Hilbert.

Tuy nhiên, năm 1997, Viện Max Planck nghiên cứu Lịch sử Khoa học tại Berlin, trong một đề án về lịch sử thuyết tương đối rộng, và dưới sự chủ trì giám đốc GS Jürgen Renn, đã tiến hành một cuộc khai quật quy mô vào kho tư liệu quan trọng của Hilbert ở Göttingen – may mắn thay chúng vẫn còn nguyên vẹn sau chiến tranh! − và mớ các “bông” (galley proofs, bản in thử để tác giả xem lại và tu chỉnh trước khi công bố chính thức) của các bài báo của Hilbert từ đó đến nay chưa được chú ý.

Kết quả cuộc khai quật đã đem lại ánh sáng hoàn toàn mới (Corry, Renn, Stachel, [1]). Sự phân tích chi ly và so sánh những bản bông này với hai phiên bản được công bố của báo cáo của Hilbert một mặt, và với các bài báo của Einstein về lực hấp dẫn từ 1913 đến 1915 mặt khác, cho phép nhóm Corry, Renn và Stachel dựng lại hồ sơ của những tuần lễ quyết định trong tháng 11, 1915, và đem lại một cái nhìn triệt để khác biệt với cái nhìn thông thường, loại bỏ hoàn toàn khả năng Einstein “đạo văn” của Hilbert. Thực tế, tình thế diễn ra hoàn toàn ngược lại: chính Hilbert mới là người đã tu chỉnh phiên bản cuối cùng của ông sau khi biết các kết quả của Einstein được công bố trước đó. Và Hilbert cũng đã thừa nhận quyền ưu tiên của Einstein.

Chi tiết: Tháng 11, 1915 là tháng quyết định. Einstein công bố 4 bài báo, trong khi ông trao đổi liên tục báo cáo và ý tưởng với Hilbert. Ngày 15. 11 ông nhận được một lá thư của Hilbert mà ông đã trả lời như sau: “Sự phân tích của ông làm tôi quan tâm ghê gớm, đặc biệt từ khi tôi nặng óc để thiết lập cây cầu giữa lực hấp dẫn và lực điện từ.” Ông xin Hilbert một bản sao, nhưng từ chối lời mời của Hilbert đi Göttingen để nghe Hilbert trình bày báo cáo của ông. Nhưng thình lình vào ngày 18.11 sau khi nhận được bản thảo đầu tiên của một báo cáo mà Hilbert sẽ công bố sớm, Einstein đổi giọng. Einstein từ chối tính chất mới mẻ và yêu sách ưu tiên của Hilbert: “Hệ thống (phương trình) ông đưa ra, trong chừng mực tôi hiểu, hoàn toàn trùng khớp với hệ thống tôi đã tìm thấy trong những tuần trước, và đã được nộp cho Hàn lâm viện”. Tức chẳng có gì mới mẻ cả. Để có thể yêu sách quyền ưu tiên của chính mình, Einstein giải thích cho Hilbert, rằng ông đã “chỉ xem các phương trình trường hiệp biến tổng quát khả dĩ ba năm trước.” Ông cũng nói bóng gió rằng Hilbert không hề thảo luận những vấn đề vật lý căn bản mà các phương trình này nêu lên:

Cái khó khăn không phải là tìm ra các phương trình hiệp biến tổng quát cho g^µv; điều này là dễ dàng với sự giúp đỡ của tenxơ Riemann. Cái thực sự khó khăn là nhận ra rằng những phương trình này làm thành một sự tổng quát hóa, và, tức là, một sự tổng quát hóa tự nhiên và đơn giản của định luật Newton.

Sau cùng, Einstein thông báo cho Hilbert biết cùng ngày ông đã nộp cho Hàn lâm viện (ngày 18 tháng 11):

Một báo cáo trong đó tôi suy ra từ thuyết tương đối rộng, một cách định lượng, mà không cần đến các giả thuyết phụ, chuyển động điểm cận nhật của Sao Thủy (Mercury) được khám phá bởi Le Verrier. Không thuyết hấp dẫn nào cho đến nay làm được điều đó.

Einstein làm được điều đó mà chưa có bộ phương trình trường cuối cùng, chỉ cần các phương trình đúng trong chân không như một trường hợp đặc biệt, đủ để cho ông tính toán. Điều đó càng làm cho ông càng tự tin.

Một tuần sau, ngày 25.11, chúng ta hãy ghi nhớ, Einstein nộp báo cáo của ông về các phương trình trường “với một thành phần thứ hai”, và được xuất bản ngày 2 tháng 12, 1915 (hãy ghi nhớ) tại Hàn lâm viện Phổ ở Berlin (Königlich Preußische Akademie der Wissenschaften). Đó chính lại là các phương trình mà Hilbert dường như đã đưa vào công bố ngày 20 trước đó. Thành phần thứ hai đó là số hạng chéo, lại xuất hiện trong bài báo Hilbert nộp ngày 20 này, và được xuất bản cuối tháng 3, 1916, trong báo Göttingen Nachrichten của Đại học Göttingen. Chính điều này đặt ra nghi vấn. Nhưng làm sao được khi mà, trong ghi chú đầu tiên của bài báo ông, Hilbert nói ông đã tham khảo tất cả những bài báo của Einstein, đặc biệt bài báo cuối cùng ngày 25? Bản bông đầu tiên của bài báo của Hilbert cho thấy lý thuyết mà ông nộp đầu tiên không có tính chất hiệp biến tổng quát, và không chứa đựng dạng rõ ràng (explicit form) của các phương trình trường của thuyết tương đối rộng. ([1] hoặc [5]) Chú ý: thời gian giữa nộp bài, ngày 20. 11.1915, và công bố bài, ngày 31. 3.1916 của Hilbert là quá lâu, đến hơn bốn tháng, lâu một cách bất thường! Rõ ràng, Hilbert cần nhiều thời gian để tu chỉnh và bổ sung cho phù hợp, trong khi kết quả của Einstein được xuất bản chỉ một tuần sau khi nộp.

Và trong bản thảo gốc của Hilbert, được tìm thấy trong cuộc khai quật kho lưu trữ của Hilbert tại Göttingen nói trên, người ta không tìm thấy các phương trình trường Einstein. Sự thật là Hilbert đã làm một số tu chỉnh vào báo cáo đề ngày 20 của ông, và ngày 20 này được ghi vào bản in sau đó, mà không ghi ngày tháng tu chỉnh về sau. Trong phiên bản in của bài báo cáo này của ông ngày 31 tháng 3 năm sau, người ta thấy Hilbert đã thêm vào một ý về bài báo cuối cùng (ngày 25.11) của Einstein, và trực tiếp nhìn nhận quyền ưu tiên của Einstein: “Các phương trình vi phân hình thành như thế (trong bài báo này) của thuyết hấp dẫn là, theo ý tôi, khớp với Thuyết tương đối rộng của Einstein được ông thiết lập tráng lệ trong những bài nghiên cứu sau cùng.” ([1]) hay ([2], hoặc xem Ảnh số 2 dưới đây)

Như thế thì đã rõ: Ban đầu Hilbert không đưa ra dạng rõ ràng của các phương trình trường; rồi sau khi Einstein công bố các phương trình trường của ông, Hilbert đã tu chỉnh bài ông cho phù hợp với các kết quả của Einstein ([5]). Nếu Hilbert chỉ thay đổi dòng ngày tháng như thế này: “nộp ngày 20 tháng 11, 1915, tu chỉnh ngày (một ngày nào đó sau ngày 2 tháng 12, 1915, là ngày công bố của bài báo kết luận cuối cùng của Einstein)” thì sẽ không có tranh luận về quyền ưu tiên diễn ra. ([4]) Như vậy cuộc tranh cãi quyền ưu tiên được kết thúc: Einstein chính là người cha đẻ của các phương trình trường và của thuyết tương đối rộng mà ông đã thai nghén từ năm 1907.

Phương trình trường về sau được Einstein viết lại

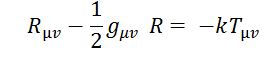
(tenxơ của độ cong không-thời gian) = hằng số x (tenxơ của sự phân bổ khối-năng lượng)

(Trong đó, R_µv là tenxơ độ cong, g_µv là tenxơ metric tượng trưng cho các thế hấp dẫn, T_µv là tenxơ (ứng suất-) năng lượng của vật chất, cho biết sự phân bổ của khối lượng trong không gian. R là vết (trace), hay số hạng chéo, tổng các thành phần nằm trên đường chéo của g_µvR_µv. Vế thứ hai bên trái còn được gọi là tenxơ Einstein, ký hiệu E_µv.)

Như vậy, ngày 25 tháng 11 năm 1915 có thể được xem là ngày chào đời của các phương trình trường, và của thuyết tương đối rộng của Einstein. Ngày 26 tháng 11, ông viết thư Zangger, bạn ông, rằng “lý thuyết có một vẻ đẹp ngoại hạng. Nhưng chỉ có một người thật sự hiểu nó, và người đó đang tìm cách “có phần” trong đó một cách khôn ngoan.” Ông ám chỉ Hilbert. Đến ngày 20 tháng 12, 1915, tức khoảng một tháng sau, và gần ba tuần sau khi báo cáo ông được chính thức in ra (trong khi báo cáo của Hilbert thì vẫn chưa xuất bản), có lẽ vui mừng trước sự thành công mỹ mãn, giải phóng ông khỏi bao sự lo lắng của tám năm trời, sự tức giận của Einstein đã dịu xuống khiến Einstein đưa ra những lời hòa giải:

Có một sự bực bội giữa chúng ta, mà nguyên nhân của nó tôi không muốn phân tích thêm. Tôi đã chiến đấu chống lại cảm giác cay đắng xuất phát từ đó, và hoàn toàn thành công. Tôi tiếp tục nghĩ đến ông với một sự thân ái không suy giảm, và tôi xin ông cũng cố gắng làm điều đó đối với tôi. Một cách khách quan, thật là đáng tiếc nếu hai người bạn, vốn đôi chút đã giải phóng mình ra khỏi thế giới hư xấu này, lại không đem lại niềm vui cho nhau.

Einstein thật ra đánh giá Hilbert rất cao. Mùa hè năm 1915, Einstein đã đến thăm Göttingen, kinh đô toán học của nước Đức, nếu không phải là của cả thế giới, theo lời mời của Hilbert sau khi Hilbert bày tỏ sự quan tâm đến thuyết hấp dẫn. Einstein lưu lại đó từ ngày 29 tháng 6 đến ngày 7 tháng 7, và trình bày ở đó một loạt sáu bày giảng, trước sự có mặt của nhiều nhân vật quan trọng, như Felix Klein, khoa trưởng khoa toán, Emmy Noether, nhà nữ toán học tên tuổi. Ông nỗ lực làm cho vật lý được chấp nhận ở kinh đô toán học này, và vui mừng trước sự tiếp nhận nồng nhiệt cách tiếp cận của ông: “Ở Göttingen tôi rất vui mừng nhìn thấy tất cả mọi thứ đểu được hiểu tường tận đến chi tiết. Tôi rất thích thú về Hilbert. Một con người quan trọng. Tôi rất tò mò về ý kiến của ông. ” Ông “có thể thuyết phục Hilbert về thuyết tương đối rộng” và khen Hilbert là “con người có một năng lượng đáng ngạc nhiên và có tính độc lập cao trong mọi thứ.” ([6] và [2]) Đó là con người có kiến thức mênh mông trong toán học, so với kiến thức nhỏ bé của Einstein học được một cách chật vật, và đang quan tâm đến vật lý, và là người duy nhất có thể qua mặt ông trong những giây phút định mệnh chót.

Hilbert được trích dẫn nói rằng: “Mỗi cậu học sinh trên đường phố Göttingen của chúng ta hiểu về hình học bốn chiều còn nhiều hơn Albert Einstein. Mặc dù thế, Einstein là người đã làm nên tác phẩm chứ không phải các nhà toán học.” ([7], 69)

Trong lá thư gửi cho Arnold Sommerfeld ngày 9.12, Einstein viết: “Ông hãy xem nó đi, đó là khám phá có giá trị nhất mà tôi đã tìm được trong suốt cuộc đời tôi.” (Xem thêm [7] và [8])

Einstein ở tuổi 36 khi hoàn tất thuyết tương đối rộng năm 1915

David Hilbert khoảng cùng thời gian

Trang đầu của một mớ bông của thông báo đầu tiên của Hilbert, 
với các tu chỉnh viết tay của chính Hilbert (“được Einstein đưa ra”)
và một con dấu của nhà in, đề ngày 6 tháng 12, 1915

(Ảnh của Viện Max Planck nghiên cứu lịch sử khoa học tại Berlin).

Minh họa Hilbert và Einstein trong cuộc chạy đua (Gutfreund và Renn, [4], 32)

Trang thứ 12 của báo cáo được công bố của Hilbert, trong đó ông viết, đoạn thứ hai từ trên xuống:
“Các phương trình vi phân hình thành như thế (trong bài báo này) của thuyết hấp dẫn là, theo ý tôi,
khớp với Thuyết tương đối rộng của Einstein được ông thiết lập tráng lệ trong những bài nghiên cứu sau cùng.”

(Ảnh của Viện Max Planck nghiên cứu lịch sử khoa học tại Berlin)

Năm 1936, Einstein mô tả phương trình trường như sau: “Lý thuyết…giống như một tòa nhà, một cánh của nó được làm bằng đá cẩm thạch tinh tế (cánh trái của phương trình), nhưng cánh khác của nó thì đươc xây dựng bằng gỗ chất lượng thấp (cánh phải của phương trình). Cách biểu diễn hiện tượng luận của vật chất, thực tế, chỉ là một sự thay đổi thô thiển cho một cách biểu diễn đem lại công bằng cho tất cả tính chất đã biết của vật chất.” (Gutfreund và Renn, [4], 103)

Một lý thuyết ra đời rất lạ lùng. Làm sao có thể thiết lập được một lý thuyết như thuyết tương đối rộng có độ áp dụng bao trùm rộng nhiều lãnh vực, từ vũ trụ giãn nở, sóng hấp dẫn đến lỗ đen, những thứ chỉ sau này mới được biết đến? Làm sao Einstein có thể thiết lập những tiêu chuẩn (criteria) cho phương trình trường hấp dẫn nhiều năm trước khi ông xác lập được giải đáp? Làm sao ông thiết lập được một khung hỗ trợ khám phá (heuristic) để dẫn ông đến một sự xác lập toán học chính xác? Đó là thuyết gian khổ nhất cho Einstein. Sau đó ông bị kiệt quệ (ziemlich kaputt).

Nhưng những nghiệm số của phương trình Einstein còn lạ lùng hơn. Người nhanh chóng đưa ra nghiệm số đầu tiên, cũng là một nghiệm số làm nên lịch sử, là nhà vật lý thiên văn Đức Karl Schwarzschild, cũng là một thành viên của Hàn lâm viện. Ngày 22 tháng 12, 1915, nghĩa là chỉ khoảng ba tuần sau khi phương trình trường Einstein được chính thức công bố, từ mặt trận Nga ông gửi về cho Einstein nghiệm số chính xác cho trường hợp một khối lượng có dạng hình cầu và không quay. Einstein rất đỗi ngạc nhiên và thích thú. Nhưng Schwarzschild mất ngay năm sau (!) chỉ mới 43 tuổi, như một vì sao vụt sáng rồi vụt tắt. Nghiệm số Schwarzschild sau này trở thành nền tảng nghiên cứu lỗ đen, và cho nghiên cứu các hệ lụy vật lý thiên văn của thuyết tương đối rộng. Thật hết sức lạ lùng.

Xin nói tiếp về năm 1916. Có hai việc. Thứ nhất, Einstein tiếp tục có thêm 17 công bố, trong đó có quyển sách Thuyết tương đối dưới đây, công trình về Sóng hấp dẫn (Approximative Integration of the Fields of Gravitation), và hai công trình quan trọng về thuyết lượng tử, “Emission and Absorption of Radiation in Quantum Theory” và “On the Quantum theory of Radiation”, trong đó ông đặt nền tảng cho ánh sáng laser, cũng như suy ra được định luật bức xạ của Planck. Đó là một đóng góp quan trọng vào thuyết lượng tử. “Một ý tưởng sáng chói đã đến với tôi về sự hấp thu và phát xạ bức xạ…Một sự suy ra (derivation) đơn giản một cách ngạc nhiên, tôi muốn nói đó là sự suy ra của công thức Planck” và “Do đó, (tính chất) quanta của ánh sáng xem như được thiết lập”, như ông viết một cách hào hứng trong một lá thư cho Besso. Mặt khác, cuối năm, ông thai nghén một công trình về ứng dụng của thuyết tương đối rộng vào vũ trụ học (cosmological considerations) với hằng số vũ trụ lambda được đưa thêm vào, để công bố ngay đầu năm 1917. Người ta bảo, 1916 là một annus mirabillis thứ hai của ông. Sự làm việc và sáng tạo của Einstein là phi thường. Tất cả những thành quả đó lại diễn ra trong lúc chiến tranh đang tàn phá châu Âu, và trong sự cô lập của Einstein đối với phần lớn các đồng nghiệp vì ông là một trong ít người lên án công khai cuộc chiến, và trong sự cô đơn khi hôn nhân của ông gãy đỗ, và hai con ông trở về Zurich cùng với Mileva.

Thứ hai, sau khi kết thúc Thuyết tương đối rộng, Einstein liền bắt tay vào soạn thảo một quyển sách cho “đại chúng” về thuyết tương đối rộng và hẹp. Tháng 1, 1916, ông viết cho bạn ông Besso: “Sự thành công lớn với lực hấp dẫn làm cho tôi vô cùng hài lòng. Tôi đang xem xét một cách nghiêm túc việc viết một quyển sách trong tương lai gần về thuyết tương đối hẹp và rộng, mặc dù, cũng như đối với tất cả những việc không được hỗ trợ bằng một ham muốn cháy bỏng, tôi có khó khăn để khởi động. Nhưng nếu tôi không làm thế, lý thuyết sẽ không được hiểu, một cách đơn giản, mặc dù nó là thế.”

Einstein hoàn tất bản thảo tháng 12, và quyển sách Thuyết tương đối hẹp và rộng, Über die spezielle und die allgemeine Relativitätstheorie, (viết cho đại chúng) là một thành công lớn. Từ 1917 – 1922, sách được in 14 lần bằng tiếng Đức. Sau khi độ lệch ánh sáng được xác nhận năm 1919, quyển sách được dịch sang tiếng Anh và nhiều thứ tiếng khác, trong đó có tiếng Nhật và tiếng Hoa (1921 và 1922).

Trong lời nói đầu của phiên bản tiếng Czech năm 1923 của quyển sách, Eintein nhắc lại những ngày sống và làm việc đầy kỷ niệm của mình tại Prague:

Tôi vui mừng khi thấy rằng quyển sách nhỏ này...sẽ ra mắt bằng ngôn ngữ mẹ đẻ của đất nước mà ở đó tôi đã tìm thấy được sự tập trung cần thiết để phát triển ý tưởng căn bản của thuyết tương đối rộng mà tôi đã thai nghén từ 1908 [ông nhầm với 1907]. Trong những căn phòng yên tĩnh của Viện Vật lý Lý thuyết của Đại học Đức Prague đường Vinicna, tôi đã khám phá rằng nguyên lý tương đương (equivalence principle) có hệ quả gây ra sự lệch của các tia sáng gần mặt trời với một độ lệch...Tại Prague tôi cũng đã khám phá sự lệch của các vạch quang phổ về phía đỏ...

Tuy nhiên, ý tưởng có tính quyết định của sự tương tự (analogy) giữa sự xác lập toán học (mathematical foundation) của lý thuyết và thuyết bề mặt (theory of surfaces) của Gauss chỉ đến với tôi năm 1912 sau khi tôi trở về Zurich, mà tôi không hề có ý thức về công trình của Riemann, Ricci và Levi-Civita tồn tại vào thời điểm đó. Người gây cho tôi ý thức về việc này là người bạn Grossmann của tôi. ([4], 9)

Einstein không những là nhà nghiên cứu, mà còn là một “nhà truyền giáo của khoa học”. Không những thế, sau chiến tranh thế giới thứ nhất, và sau khi thuyết tương đối rộng được kiểm chứng trên trời, Einstein còn là “nhà truyền giáo của hòa bình và hòa giải các dân tộc”. Không một gương mặt nào khác có đủ uy tín, đủ tên tuổi, và đủ sức hút, để làm chuyện ấy ngoài Einstein. (Xem thêm [7])

Quyển sách Thuyết tương đối đã trở thành một classic của thế giới. Tại Việt Nam, mãi đến năm 2014, bản tiếng Việt của quyển sách này lần đầu tiên ra mắt, tức sau gần 100 năm “lệch giờ” (xem ảnh). Âu điều đó cũng nói lên sự tụt hậu quá lâu về khoa học của VN. (Xem Lời dẫn nhập trong [8])

Cám ơn. Tác giả cám ơn GS Phạm Xuân Yêm, TS Nguyễn Trọng Hiền, và GS Jürgen Renn của Viện Max Planck nghiên cứu lịch sử khoa học tại Berlin đã cho những góp ý và tư liệu quý báu.

Tài liệu tham khảo

[1] Leo Corry, Jürgen Renn, John Stachel, Belated Decision in the Hilbert-Einstein Priority Dispute, trong Science 14 Nov 1997, vol. 278, Issue 5341, pp. 1270-1273.

[2] Jean Eisenstaedt, The Curious History of Relativity. How Einstein’s Theory of Gravity Was Lost and Found Again. Princeton Press, 2006.

[3] Jürgen Renn, Learning from Einstein: Innovation in Science. Trong Peter L. Galison, Gerald Holton, Silvan S. Schweber (eds), EINSTEIN for the 21^st Century. His legacy in science, art, and modern culture. Princeton University Press, 2008.

[4] Hanoch Gutfreund và Jürgen Renn, The Road to Relativity. The History and Meaning of Einstein’s “The Foundation of General Relativity”. Princeton University Press, 2015.

[5] Leo Corry, Jürgen Renn, John Stachel, được trình bài lại trong John Stachel (ed), Einstein from ‘B’ to ‘Z’. Einstein studies, Volume 9. Birkhäuser 2002. Trang 339-346.

[6] John Stachel (ed), Einstein from ‘B’ to ‘Z’. Einstein studies, Volume 9. Birkhäuser 2002.

[7] Nguyễn Xuân Xanh, EINSTEIN. NXB Tổng hợp Thành phố, 2016.

[8] Albert Einstein, Thuyết tương đối hẹp và rộng. Nguyễn Xuân Xanh dịch và viết lời dẫn nhập. NXB Tổng hợp Thành phố, 2014.

(2) 

Một phát biểu về Phật giáo được cho là của Einstein

Ngộ nhận thứ hai xoay quanh một phát biểu liên quan đến Phật giáo được lưu truyền rất lâu trên mạng, được xem như là phát biểu chính thức của Einstein mà không có nguồn gốc rõ ràng, chỉ thấy trích qua trích lại. Một phiên bản của lời trích này là:

Phật giáo có những tính chất đặc trưng của một học thuyết được chờ đợi trong (khuôn khổ) một tôn giáo vũ trụ cho tương lai: nó vượt lên một đấng Thiên Chúa có hình người, tránh được các giáo điều và thần học; nó bao trùm cả hai phần, tự nhiên và tâm linh; nó được xây dựng trên ý thức tôn giáo với niềm khao khát muốn trải nghiệm tất cả mọi thứ, tự nhiên và tâm linh, như một sự thống nhất đầy đủ ý nghĩa. Phật giáo đáp ứng các tính chất này. Nếu có một tôn giáo đáp ứng những nhu cầu khoa học hiện đại, thì đó là Phật giáo.

Đó là phiên bản gần đây nhất mà vào một ngày nọ tháng 3 năm 2014, GS Cao Huy Thuần ở Paris “báo động” cho tôi biết rằng nó nằm trong quyển sách Perry Garfinkel, Buddha or Bust, nxb Harmony, 2007, trang 15. Nguyên văn tiếng Anh ở đó:

Trích dẫn nguồn gốc đây rồi! Nhưng lại rất ngạc nhiên, vì tôi đã đọc quyển sách The Human Side từ lâu, nhưng đâu thấy đoạn trên ở đâu. Quyển The Human Side gần đây cũng đã được dịch sang tiếng Việt, dưới tên Albert Einstein, Mặt Nhân Bản, mọi người có thể tham khảo:

Perry Garfinkel là một nhà báo không phải vô danh, ông viết cho nhiều tờ báo lớn, trong đó có New York Times. Quyển Buddha or Bust được giới thiệu trên trang bìa là một “National Bestseller”, và bên trong có trích lời khen của Đức Dalai Lama, Thiền sư Thích Nhất Hạnh, của tờ The Boston Globe, và vài nhân vật khác. Đoạn trích dẫn trên thực ra không liên quan gì đến nội dung chính của quyển sách mà các lời khen có lẽ đã dành tặng. Nhưng ai đọc câu trích dẫn của Einstein cũng sẽ có ấn tượng mạnh. Sự không đúng thật này sẽ tiếp tục lan tỏa, và người đọc sẽ không biết rằng đoạn trích dẫn nói trên là không có thật.

Tôi cũng đã từng lùng sục nhiều sách vở viết về Einstein, đặc biệt những quyển sách viết chuyên về quan điểm tôn giáo của ông, như quyển Max Jammer, Einstein and Religion, để tìm dấu vết ý tưởng trên, nhưng tuyệt nhiên không thấy câu nói nào của Einstein có nội dung giống như thế. Tôi cũng liên lạc với Kho lưu trữ Albert Einstein của Đại học Hebrew ở Jerusalem là nguồn thông tin phong phú nhất. Nhưng họ cũng không biết có phát biểu nào như thế của Einstein.

Einstein ngưỡng mộ Phật giáo, điều đó chắc chắn. Ông có một phát biểu trong quyển sách Thế giới như tôi nhìn của ông như sau, và có lẽ đây là “cảm hứng” cho ý tưởng trên của Garfinkel:

Mạnh mẽ hơn nhiều là các yếu tố mang tính tôn giáo vũ trụ trong Phật giáo, những điều mà các tác phẩm tuyệt vời của Schopenhauer đã dạy cho chúng ta. Các thiên tài tôn giáo của mọi thời đại đều được đặc trưng bởi tính tín ngưỡng vũ trụ (cosmic religiosity), tính chất không hề để ý đến các giáo điều hay một Thiên Chúa được tạc theo hình ảnh của con người.

(Bài Tôn giáo và Khoa học)

Hoặc trong Mặt Nhân Bản, tr. 73:

Thời đại chúng ta được làm cho khác biệt bởi những thành tựu tuyệt vời trong những lĩnh vực hiểu biết khoa học và ứng dụng kỹ thuật của những nhận thức sâu sắc đó. Ai mà không vui sướng bởi điều này? Nhưng đừng quên rằng, chỉ tri thức và kỹ năng thôi không thể dẫn dắt loài người đến một cuộc sống hạnh phúc và có phẩm giá được. Những người khai sinh ra các chuẩn mực và giá trị đạo đức cao quý luôn xứng đáng được nhân loại đề cao hơn những người khám phá ra chân lý khác quan…. Những gì nhân loại chịu ơn những nhân cách như Đức Phật, Moses và Jesu đối với tôi còn cao hơn tất cả thành tựu của những bộ óc khám phá và phát minh.

Chúng ta phải bằng hết sức mình bảo vệ và giữ cho sống mãi những gì mà những con người thiêng liêng này đã trao tặng chúng ta, nếu nhân loại không muốn đánh mất phẩm giá, sự tồn tại yên bình và niềm vui trong cuộc sống. (1937)

Tôi rất mong, ai tìm được nguồn gốc trích dẫn liên quan đến Phật giáo nói trên xin vui lòng xác nhận giùm, như nguồn trích dẫn của nó, Einstein đã phát biểu trong dịp nào, hay trong thư viết cho ai, và ngày tháng năm nào để mọi người có thể truy lại trong The Collected Papers of Albert Einstein. Cho tới lúc đó, chúng ta vẫn nên hiểu rằng trích dẫn trên, hay những trích dẫn có nội dung tương tự, rất tiếc, là chưa đúng sự thật. Chúng ta không muốn làm gì hơn là tìm về sự thật.

Trước khi kết thúc, tôi xin kể thêm ý tưởng sau đây của một người khác nói về Phật giáo và khoa học. Vị viện trưởng người Anh, Greg Whitefield, của Viện Phật học Rangjung Yeshe Institute ở Nepal, được thành lập từ 2002 bởi vị lama Tây Tạng Tulku Chokyi Nyima Rinpoche. Ông viết: “Tôn giáo tương lai của nhân loại sẽ được dựa lên các định luật khoa học. Phật giáo là rất khoa học vì nó dựa lên các định luật nhân quả.”

Chưa biết tương lai như thế nào, nhưng ở đây tôi chỉ muốn nói vế thứ hai. Đức Phật dạy thuyết nhân-quả đã mấy ngàn năm. Nhưng trong lãnh vực y học, thuyết này thực sự mới thắng lợi trọn vẹn trong cuộc cách mạng vĩ đại do Louis Pasteur và Robert Koch dẫn đầu trong thập niên 1880, nghĩa là mới khoảng 150 năm trước thôi, khi hai người khổng lồ này chứng minh bằng khoa học rằng các bệnh đều do các vi sinh vật nhỏ bé gây ra mắt thường không nhìn thấy. Có mầm bệnh mới sinh ra bệnh (Koch), cũng như có vi sinh vật mới có những quá trình như lên men, hay thối rữa (Pasteur). Hằng loạt mầm bệnh được phát hiện, như bệnh than, bệnh lao, dịch tả, dại, bạch hầu v.v. cùng với các liệu pháp điều trị. Điều đó ngày nay được xem là hiển nhiên, nhưng hàng ngàn năm nhân loại đã không thể chứng minh được. Có lẽ đó là sự khẳng định cuối cùng của thuyết nhân quả trong thế giới khoa học, chấm dứt mọi tư biện thần bí. Xin xem chi tiết về cuộc cách mạng y học này trong quyển sách sắp tới có tên “Pasteur-Koch. Cuộc đọ sức giữa những người khổng lồ trong thế giới vi sinh vật” của NXB Tổng hợp Thành phố.

Nguyễn Xuân Xanh

Tháng 5, 2017