Phỏng vấn nhà toán học Nguyễn Quang Đỗ Thống

Từ Pierre de FERMAT
đến Andrew WILES

Bất tri tam bách dư niên hậu, thiên hạ hà nhân ... chứng Fermat! Từ hơn ba trăm năm nay, các nhà toán học, chuyên nghiệp hay tài tử, đã hoài công chứng minh “định lý Fermat”...

Cuối tháng 6.93, các báo đưa tin : nhà toán học Anh, Andrew WILES đã chứng minh thành công định lý này. Dưới đây, chúng tôi phỏng vấn nhà  toán học Nguyễn Quang Đỗ Thống, cựu học sinh Ecole Polytechnique, giáo sư Trường đại học Besançon, một trong vài ba trung tâm toán học Pháp chuyên về ngành lý thuyết số.

Câu hỏi và câu trả lời nhằm thoả mãn nhu cầu tìm hiểu thời sự khoa học của bạn đọc ngoài nghề, chỉ cần trình độ trung học phổ thông. Câu nào đoạn nào có vẻ chuyên môn, bạn đọc chỉ cần lướt qua.

Diễn Đàn (DĐ): Cuối tháng 6, báo chí thế giới, trong đó phải kể những tờ báo có uy tín lớn (Le Monde ở Paris, The Times ở London, The New York Times...) đã đưa tin trang nhất: A. Wiles đã chứng minh “định lý cuối cùng của Fermat”. Có lẽ đây là lần đầu tiên mà toán học thuần tuý trở thành đề tài thời s ự hàng đầu. Tại sao vậy? Và trước tiên, xin anh tóm tắt cho độc giả Diễn Đàn định lý Fermat và lịch sử, có thể nói huyền sử, của nó.

Nguyễn Quang Đỗ Thống (NQĐT): Định lý Fermat!... Đã gần 350 năm nay nó ám ảnh giấc ngủ, giấc mơ của các nhà toán học – và kỳ lạ hơn – nó ám ảnh cả trí óc của những người ngoại đạo. Có thể nói không ngoa: định lý Fermat đã trở thành huyền thoại. Sở dĩ nó được nhiều người biết đến như vậy là do sự kết hợp của nhiều yếu tố: nó được khai sinh một cách lãng mạn, phát biểu một cách hết sức đơn giản, dễ hiểu, thế mà muốn chứng minh nó, thì khó khăn vô cùng... Các em học sinh trung học đều nghe kể chuyện về định lý Fermat: trong các di cảo của Pierre de Fermat (1601-1665), người ta tìm thấy một tác phẩm của Diophante do Bachet xuất bản, ngoài lề những trang sách, có bút tích của Fermat. Diophante là một nhà hình học thời Cổ Hy Lạp. Ông đã khai sáng ra một lãnh vực toán học mà ngày nay, người ta gọi tên là phương trình Diophante, tức là những phương trình đa thức mà người ta phải tìm ra đáp số là những số nguyên. Fermat là nhà toán học xuất sắc nhất của thế kỷ 17 về lãnh vực này. Và trong ấn bản Bachet, trang nói về bài toán số 8 của Diophante (tìm tất cả những tam giác vuông mà chiều dài ba cạnh tỉ lệ với ba số nguyên), Fermat có ghi chú ngoài lề như sau: “ Ngược lại, không thể nào phân tích lập phương của một số nguyên thành tổng số của hai lập phương, và nói chung, không thể phân tích luỹ thừa (bậc 3 trở lên) của một số nguyên thành tổng số hai luỹ thừa cùng bậc: tôi đã tìm ra một cách chứng minh tuyệt vời (định lý tổng quát này) nhưng không thể viết ra đây vì thiếu chỗ”. Theo ngôn ngữ toán học hiện đại, có thể phát biểu bài toán số 8 của Diophante như sau: “Tìm các số nguyên khác không x, y, z, sao cho x² + y² = z²”. Nhìn thấy đẳng thức này, ai học trung học cũng nhớ tới định lý Pythagore (một tam giác mà ba cạnh x, y, z liên hệ với nhau bằng đẳng thức x² + y² = z² là một tam giác vuông, x và y là hai cạnh của góc vuông, còn z là đường huyền). Khó khăn của bài toán Diophante là phải tìm lời giải số nguyên. Ở Trung Quốc, từ thời thượng cổ, người ta đã biết một hình tam giác mà ba cạnh chiều dài 3, 4, 5 là một tam giác vuông, vì : 3² + 4² = 5² (3² là 3 nhân 3 = 9, 4² là 4x4 = 16; 5² = 5x5 = 25 và đúng là ta có 9 + 16 = 25). Như vậy ba số nguyên 3, 4, 5 là một lời giải, nhưng vấn đề là phải tìm ra tất cả các lời giải bằng số nguyên. Người Cổ Hy Lạp đã biết giải nhiều bài toán loại này. Các bạn, dù không làm toán, cũng nên ngồi cộng và nhân thử một loạt con số để thưởng thức cái vui của số học: định lý dễ đọc, dễ nhớ, nhưng chứng minh thì hắc búa. Trở lại “định lý” Fermat, ta có thể phát biểu nó như sau: “ Nếu n ≥ 3 thì phương trình xⁿ + yⁿ = zⁿ không có nghiệm số nguyên x, y, z mà cả ba đều khác số không”

Và từ hơn ba trăm năm nay, các nhà toán học, lớn bé trẻ già, đã tìm cách chứng minh mệnh đề đó, có người, như Gauss, âm thầm tìm kiếm, không thố lộ với ai. Tôi có thể đoán chắc là tất cả những nhà toán học nào đã chọn lãnh vực lý thuyết số (théorie des nombres), cũng đều vì duyên nợ với cái định lý tai quái này. Và một trong những nguyên nhân làm cho nhiều người chú ý đến nó là những giải được treo sẵn để tặng thưởng cho những ai chứng minh được định lý Fermat: Giải thưởng lớn của Viện Hàn lâm khoa học Pháp đặt ra từ năm 1853, và của Viện Wolfskehl bên Đức (100.000 mác, trị giá năm 1908!).

Người ta đã giải được một số trường hợp đặc biệt, và quan trọng hơn, những khái niệm mới đã được tạo ra, dẫn tới những tiến bộ lớn trong ngành lý thuyết số. Nhiều lần, người ta tưởng cuộc trường chinh đã kết thúc, mà rốt cuộc, vẫn phải cất bước tiếp tục Định lý Fermat, đối với làng toán, cũng giống như cuộc đi tìm Saint-Graal của các hiệp sĩ thời Trung cổ. Tôi còn nhớ mãi một cảnh trong phim “Chiếc ấn thứ bảy” của Ingmar Bergman: trở về sau một cuộc Thánh chiến, chàng kỵ sĩ thách thức Tử Thần đấu ván cờ với mình, để trì hoãn giờ tạ thế. Có lẽ Pierre de Fermat cũng đã tung ra “định lý cuối cùng” để thách thức Tử Thần: Tử Thần cứ loay hoay tìm cách chứng minh, và Fermat cứ an nhiên sống mãi...

DĐ : Cho đến cuối tháng 6.1993 mới chết? Nay là cuối tháng 8.93, hai tháng đã trôi qua từ ngày ông Wiles thuyết trình ở Cambridge: có thể nào khẳng định rằng định lý Fermat đã thực sự được chứng minh chưa?

NQĐT : Báo Le Monde đã đưa tin thì phải đúng chứ!... Nếu phải trả lời nghiêm chỉnh, thì xin nói như thế này:

Trong quá trình “chính thức hoá” một chân lý toán học (và rộng hơn, một chân lý khoa học) có ba cửa ải phải vượt qua. Giả sử anh nghĩ rằng mình vừa “tìm” ra một định lý hay. Cửa ải đầu: anh nói chuyện với những đồng nghiệp cùng làm việc trong bộ môn của anh. Đó là cửa ải “ informel”, không chính thức. Qua cửa ải đó rồi, anh bước sang công đoạn thứ hai, chính thức hơn: thuyết trình bài chứng minh trong một xêmina hay một khoá hội thảo (colloque), sau đó (hoặc đồng thời) soạn thành một văn bản, gọi là tiền ấn bản (preprint), và phổ biến trong giới chuyên gia để xin ý kiến. Nếu tiền ấn bản lọt qua giai đoạn phê bình này, anh phải qua cửa ải thứ ba, là gửi nó tới một tạp chí chuyên môn để xin đăng. Đây mới là giai đoạn chính thức vì bộ biên tập tạp chí sẽ cử một hay nhiều báo cáo viên ( referees), được chọn trong những nhà toán học có thẩm quyền về lãnh vực này, để họ kiểm tra luận cứ và đánh giá công trình. Họ “duyệt” xong, đồng ý công bố, nghĩa là định lý của anh được thừa nhận một cách chính thức và dứt điểm (đúng hơn, hầu như dứt điểm, vì thỉnh thoảng, cũng có bài được đăng, nghĩa là đã qua lọt cả ba cửa ải, mà vẫn còn sót lỗi). Quá trình ba cửa ải nói trên chính là hiến pháp của “ nền cộng hoà khoa học”.

Về sự kiện Wiles, tôi chỉ có thể nói thế này: ông ta đã thuyết trình ba buổi liên tiếp tại một khoá hội thảo quốc tế về các hàm số L tại Học viện Newton ở Cambridge, với sự tham gia của những chuyên gia lớn nhất, và đã gửi đăng công trình 180 trang của mình cho một tạp chí, và tạp chí này đã cử ra 5 người duyệt. Theo thời hạn thông thường, thì phải từ 6 tới 9 tháng nữa, ta mới biết chắc. 9 tháng cũng là thời gian bình thường của một cuộc thai nghén, sinh nở!

DĐ : Tóm lại là các nhà báo không thận trọng bằng giới khoa học?

NQĐT : Nhà báo Diễn Đàn nói thật chí lý. Phải nói rằng các phóng viên khoa học rất nhiệt tình với huyền thoại định lý Fermat. Cách đây bốn, năm năm, báo chí cũng vội vã đưa tin một nhà toán học Nhật Bản, Y. Miyaoka, đã chứng minh định lý này. Thực ra Miyaoka không hề nói như vậy, ông ta mới chỉ ở công đoạn thứ nhất, như tôi đã nói ở trên, chứ chưa đi xa hơn. Nếu là thời xưa, có lẽ Miyaoka đã phải lấy kiếm để tuẫn tiết! Còn A. Wiles, sau khi thuyết trình xong buổi thứ ba ở Cambridge, ông ta đã tìm cách tàng hình, nhưng không may Tivi Anh đã tìm ra nơi ẩn trú. Âu cũng là cái giá phải trả cho Fermat... Về mặt phương pháp luận, tất nhiên phải thận trọng, nhưng ngay từ bây giờ, có thể nói: lần này có lẽ là ăn chắc. Tất cả các chuyên gia đều nhất trí đánh giá: chiến lược là đúng, hậu cần là đúng, mà Wiles lại là một kiện tướng. Tài năng thì Wiles đã từng thi thố rồi: tên tuổi của ông đã ghi vào sử xanh toán học cách đây 15 năm khi ông chứng minh thành công một mệnh đề mà trong nghề toán gọi là ức đoán chủ yếu về các hàm L p-adic (conjecture principale des fonctions L p-adiques).

DĐ : Nói vậy, nhưng người ta có cảm tưởng tất cả chỉ dựa vào một nhúm nhỏ những chuyên gia, cho dù là lỗi lạc tới đâu chăng nữa . Nói cụ thể, theo anh, hiện nay trên thế giới, có bao nhiêu người có khả năng kiểm chứng công trình của Wiles? Hay, đơn giản hơn, có thể đọc và hiểu 180 trang của Wiles?

NQĐT : Tất nhiên, trong lãnh vực này, không thể xem thường ý kiến của chuyên gia. Sau bao năm “tu luyện” và “quần thảo” với định lý Fermat, có thể nói là họ đã đắc đạo tới mức đọc một bài chứng minh, bằng trực năng họ có thể cảm nhận là nó đúng hay sai. Có thể so sánh trực năng toán học của họ như lỗ tai thẩm âm tuyệt đối của một Mozart, hay Bach, nghe trình tấu một bản fugue, nốt nào chệch là họ thấy chướng tai ngay.

Anh hỏi tôi: ai có thể hiểu được bài chứng minh của Wiles? Về nguyên tắc mà nói, toán học là định nghĩa, tiên đề, diễn dịch, định lý. Cho nên, bất cứ ai cũng có thể hiểu được, miễn là phải học từ A tới Z. Tất nhiên, đó là nói nguyên tắc cho vui. Nói một cách thực tế, xin trả lời như sau: ai không ở trong nghề toán thì không thể hiểu chứng minh của Wiles; còn trong nghề toán, ai không nghiên cứu về lý thuyết số hay hình học đại số cũng không thể hiểu; trong giới các chuyên gia về hai lãnh vực vừa kể tên, có chừng vài trăm nhà toán học có thể hiểu được hai nguyên lý lớn của bài chứng minh; và trong số vài trăm ấy, khoảng vài chục người có thể hiểu từng chi tiết. Còn nói về khả năng kiểm tra từng bước lý luận của Wiles, có lẽ chừng gấp đôi số báo cáo viên vừa được cử, nghĩa là chừng mười người. Mười người giữa thế gian hiện nay khoảng bốn tỷ người, kể ra cũng trớ trêu thật.

DĐ : Bộ phức tạp đến mức như vậy sao? Diễn Đàn vốn mang tiếng là phức tạp, nên chúng tôi xin miễn đi vào chi tiết. Nhưng muốn anh nói đại để A. Wiles đã phải dùng những công cụ nào, những ngón nghề gì để chứng minh một mệnh đề vỏn vẹn có 2 dòng, liên quan tới số nguyên, tức là những con số mà nhân loại đã biết dùng từ thời tiền sử, ít nhất từ ngày loài người chuyển từ văn minh hái lượm sang văn minh chăn nuôi, vì chăn nuôi là phải biết đếm... đầu trâu mặt ngựa: một, hai, ba, bốn?

NQĐT : Câu hỏi quá phức tạp! Tôi xin chịu, không thể trả lời, vì không thể giải thích toán học một cách phổ cập được. Tôi chỉ có thể phác hoạ mấy nét lớn của những tư trào đã hội tụ và dẫn tới công trình của Wiles. Bởi vì, theo tôi, có một điều rất đơn giản nhưng không phải là hiển nhiên đối với mọi người (nếu không thì đó chẳng xảy ra những vụ phát minh tiếu lâm như “máy bay thính mũi”, “nước lã có trí nhớ”...), đó là: tri thức mà loài người tích luỹ được đã trở thành mênh mông và phức tạp đến mức không thể có những phát minh “phép lạ”, từ trên trời rơi xuống được nữa. Xét cho cùng, điều đó cũng chưa hề xảy ra trong quá khứ. Newton đã từng nói sở dĩ ông nhìn xa thấy rộng (khi ông phát kiến ra nguyên lý vạn vật hấp dẫn, và sáng lập ra cơ học cổ điển) là vì ông đã được “ công kênh trên vai những người khổng lồ”, (ám chỉ các nhà khoa học tiền bối).

Vậy, nếu phải tóm lược (nghĩa là thiếu chính xác) những gì đã dẫn tới Wiles, có thể phân ra 4 thời kỳ lớn:

1) Từ Fermat đến năm 1857, dù các nhà toán học lớn, trong đó phải kể Euler (1707-1783), bỏ ra nhiều công sức, cũng chỉ chứng minh được một vài trường hợp cá biệt. Coi như không đáng kể.

2) 1857 là năm Viện Hàn lâm khoa học Pháp quyết định tặng Giải thưởng lớn cho E.-E. Kummer (1810-1893) để tưởng thưởng các công trình của ông về bài toán Fermat. Tuy rằng xét cho cùng Kummer chưa chứng minh được định lý tổng quát, nhưng ông đã triển khai những phương pháp mới và đã sáng lập ra bộ môn toán học mà ngày nay ta gọi là “lý thuyết đại số học về số” (théorie algébrique des nombres). Phần lớn các chuyên gia đều cho rằng không thể chứng minh được định lý Fermat nếu chỉ đơn thuần tự giới hạn trong khuôn khổ lý thuyết này, nhưng từ lâu rồi, lý thuyết này đã phát triển những bước vượt bực, và sống cuộc sống riêng của nó, độc lập với bài toán Fermat.

3) 1983 cũng là một năm bản lề: G. Faltings đã chứng minh một ức đoán về hình học đại số, gọi là “ức đoán của Mordell”: “mọi đường cong thuộc loại từ 1 trở lên chỉ có một số hữu hạn những điểm hữu tỷ” (Toute courbe de genre supérieur ou égal à un n’a qu’un nombre fini de points rationnels). Thế mà một đường cong của phương trình Fermat cấp n, với n ≥ 3, loại của nó là (n – 1) (n – 2)/2, nghĩa là ít nhất cũng thuộc loại 1, cho nên phương trình Fermat chỉ có một số h ữu hạn đáp số là số nguyên (tất nhiên, định lý Fermat nói rõ con số này là số 0). Cũng xin mở ngoặc để nói là đối với nhiều nhà toán học, công trình 1973 của Faltings là “định lý thế kỷ”, thứ định lý trăm năm một thuở, sâu sắc hơn hẳn định lý Fermat. Từ đó đến nay, nhiều nhà toán học, trong đó có Miyaoka (đã nói ở trên), đã tìm cách cải tiến định lý Faltings để từ đó suy ra định lý Fermat, nhưng họ đều thất bại, và dường như các chuyên gia không đi theo hướng này nữa.

4) Điều kỳ thú là Wiles đã chọn một con đường vòng, có thể dùng thuật ngữ nghệ thuật là baroque. Trong thập niên 1980, G. Frey đã bày trò bằng cách giả sử rằng định lý Fermat là sai, nghĩa là phương trình Fermat có đáp số. Từ đáp số giả định đó, Frey “vẽ” nên được một đường cong elliptic (nghĩa là đường cong loại 1). Trò chơi trở thành chuyện nghiêm chỉnh khi làng toán khám phá ra rằng đường cong giả định đó mâu thuẫn với “ức đoán của Taniyama-Weil”. Nói cách khác, nếu chứng minh được rằng “ức đoán của Taniyama-Weil” là đúng, thì đương nhiên là không thể có đường cong giả định, mà đã không có đường cong ấy, thì định lý Fermat không sai, nghĩa là đúng. Tóm lại, muốn chứng minh định lý Fermat, chỉ cần chứng minh “ức đoán của Taniyama-Weil”.

Dường như A. Wiles đã chứng minh được một phần ức đoán của T.W.: ông ta không chứng minh được ức đoán T.W. cho tất cả các đường cong elliptic, mà chỉ cho riêng những đường cong elliptic nửa ổn định, nhưng như vậy cũng đủ để đi tới hệ quả là định lý Fermat!

Có thể nói thêm: định lý Wiles thâm thuý hơn và lý thú hơn hẳn bài toán Fermat.

Để chứng minh được định lý của mình, Wiles đã phải huy động toàn bộ những thành tựu ba mươi năm qua trong lãnh vực các “dạng modula” (mà Wiles là một trong những chuyên gia cự phách) và những lãnh vực phụ cận. Nếu phải kể đến nền tảng chung của các lãnh vực này, thì có thể nói không một chút cường điệu: Wiles đã vận dụng toàn bộ lý thuyết số từ ngày Kummer sáng lập!

DĐ : Nếu vậy thì có thể tự hỏi có thật là Fermat đã chứng minh được định lý đó không...

NQĐT : Fermat là nhà toán học lớn nhất của thời đại ông. Hồi thế kỷ 17, không có những nhà toán học chuyên nghiệp: Fermat bình sinh là thẩm phán, Descartes là triết gia, còn Pascal thì... đi tu ở dòng Jansen. Toán học là trò tiêu khiển những khi nhàn tản, định lý là những câu đố mà người ta mang ra thách nhau chứng minh. Fermat hầu như chưa hề công bố một chứng minh nào của ông. Nhưng mỗi lần Fermat phát biểu một định lý, đời sau đều chúng minh được cả, có khi phải chật vật lắm mới làm được (Euler đã mất 7 năm mới chứng minh được định lý Fermat “mỗi số nguyên tố dưới dạng 1 + 4n có thể viết thành tổng của hai số nguyên bình phương, và cách viết đó là duy nhất”). Mệnh đề sai duy nhất của Fermat là mệnh đề liên quan tới những số nguyên tố gọi là “số Fermat” (tức là những con số thuộc dạng 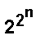 + 1, Fermat tưởng rằng chúng đều là số nguyên tố; điều đó sai đối với con số khổng lồ là 4 294 967 297 = 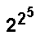 + 1), song Fermat cũng chỉ nêu mệnh đề này như một giả thuyết (hypothèse), chứ không quả quyết đó là định lý (théorème). Do đó mà uy tín của Fermat đối với người đương thời cũng như đối với đời sau vô cùng to lớn. Tuy nhiên, ngày nay, phần đông các chuyên gia cho rằng nếu Fermat đã tìm ra một chứng minh cho định lý cuối cùng, thì chứng minh đó chắc cũng sai. Một trong những người phản bác ý kiến này là G. Terjanian (ở Toulouse), năm 1977 đã đưa ra một chứng minh “sơ đẳng” (dài vỏn vẹn có 3 trang) về định lý Fermat trong trường hợp số mũ n là một số chẵn. Chữ “sơ đẳng” xin hiểu một cách tương đối, vì “sơ đẳng” cũng có ba bảy cấp. Hàng năm, Hàn lâm viện khoa học Pháp đều nhận được hàng tá những chứng minh do các nhà toán học tài tử gửi tới: những chứng minh “sơ đẳng” chỉ dùng các phép tính “sơ đẳng” là cộng (trừ) nhân (chia) đều chắc chắc là vô hiệu (điều này có thể dùng khái niệm “số nguyên p-adic” để minh chứng).

DĐ : Anh đã nhấn mạnh tới vai trò động lực của bài toán Fermat trong quá trình phát triển của toán học, nhất là của số học. Bây giờ (coi như) bài toán đã được giải, thì toán học lấy gì làm động lực. Còn bao nhiêu ức đoán vẫn đợi chờ những A. Wiles để trở thành định lý được chứng minh?

NQĐT : Đúng là từ nay các nhà toán học sẽ cảm thấy ít nhiều trơ trọi, côi cút. Nghe tin mừng truyền đi từ Cambridge, tôi tin chắc tôi không phải là người duy nhất cảm thấy trống trải trong lòng. Một cuộc tìm kiếm kéo dài hơn ba thế kỷ nay đã kết thúc, một giấc mơ trở thành hiện thực, một khát vọng cuồng nhiệt bỗng nhiên viên mãn... bao giờ chẳng để lại đôi chút man mác, bâng khuâng. Ai đã từng ước mơ, ai đã từng yêu đương tất thông cảm điều tôi vừa nói. Song, bức tường Berlin sụp đổ không có nghĩa là Lịch sử đã kết thúc (như một nhà chính trị học người Mỹ gốc Nhật đã lầm tưởng). Và khi bức màn bí mật Fermat đã được vén lên, thì Toán học cũng không chấm dứt (như một vị giám khảo trong kỳ thi tuyển mùa hè vừa qua ở Pháp đã liều lĩnh tuyên bố...). Ở trên, tôi đã nói có rất nhiều ức đoán toán học còn hứng thú và thâm thuý hơn hẳn bài toán Fermat. Một số đã được chứng minh, một số khác vẫn cưỡng lại mọi cuộc tiến công và đang làm động lực cho toán học như định lý Fermat trước đây. Riêng trong ngành số học, có thể kể ra: giả thuyết của Riemann, ức đoán của Leopoldt, ức đoán của Birch và Swinnerton-Dyer... Có điều là những ức đoán đó không dễ hiểu đối với đại chúng, nên chúng sẽ không bao giờ trở thành một huyền thoại đầy hấp lực như định lý Fermat.

DĐ : Nghe nói chính anh cũng vừa chứng minh xong một ức đoán về số học?

NQĐT : Vâng. Đó là một ức đoán về các hàm L p-adic cũng khá hấp dẫn đối với các nhà chuyên môn. Nhưng tôi xin miễn đề cập nó ở đây, không phải vì muốn tỏ vẻ khiêm nhường, mà vì hai lý do: a) nó quá bí hiểm đối với người ngoài nghề, b) chứng minh của tôi đang ở cửa ải cuối cùng mà tôi nói ở trên, cho nên phải chờ đợi. Kiên trì cũng là một đức tính mà khoa học đòi hỏi.

DĐ : Câu hỏi cuối cùng, không thể không đặt ra, nhất là lúc nãy, anh đã dùng chữ trớ trêu: bao nhiêu tài năng siêu việt, bao nhiêu công sức... giá dùng vào việc khác, biết đâu lại hay hơn? Xét cho cùng, toán học để làm gì?

NQĐT : Anh đã hỏi cuội như vậy, tôi cũng có thể trả lời cuội. Theo kiểu: không thể nào biết trước được rằng toán học “thuần tuý” sẽ dẫn tới những ứng dụng thực tế gì. Các thí dụ kinh điển mà người ta thường viện dẫn là: các ngôn ngữ tin học ngày nay đang dùng trong máy tính đều bắt nguồn từ thuyết monoïd, các phương pháp mã hoá và giải mã đều dẫn xuất từ lý thuyết số. Thay vì trả lời kiểu đó, tôi xin nhắc lại một hồi tưởng. Cuối thập niên 1970, tôi có trình bày một loạt bài ở Trường đại học tổng hợp Hà Nội, lại cũng về định lý Fermat. Đó là lúc chủ nghĩa duy ý chí đang ngự trị ở Việt Nam. Khoa học kỹ thuật được tấn phong là cuộc cách mạng then chốt, đại tướng Võ Nguyên Giáp được trao trọng trách lãnh đạo khối khoa học kỹ thuật, đi đâu cũng nghe các quan chức lớn nhỏ thao thao bất tuyệt về khoa học “thuần tuý” và khoa học “ứng dụng”. Cho nên, tại Trường đại học Hà Nội, khi trong cử toạ có một vị đặt ra câu hỏi cuội như trên, tôi e là đã mất bình tĩnh, nên đã trả lời hơi thiếu ngoại giao như thế này: “ Tôi cũng không biết toán học có ích lợi gì, chỉ biết số tôi là số đỏ vì tôi được trả tiền để làm một công việc mà đằng nào người ta không trả tiền tôi cũng vẫn cứ làm!”. Hôm nay nghĩ lại, tôi biết tôi sẽ trả lời hơi khác, nghĩa là ngoại giao hơn, long trọng hơn. Tôi sẽ dùng hình ảnh alpinistes, những nhà thể thao chiếm lĩnh những đỉnh núi cao. Tôi sẽ nói như Jean Dieudonné trong tác phẩm chúc thư của ông, rằng tôi làm toán “ vì danh dự của trí tuệ con người”.

Nguyễn Quang Đỗ Thống

Thực hiện phỏng vấn và biên dịch: 

Nguyễn Ngọc Giao

Định lý Pythagore trong sách vở đời Hán

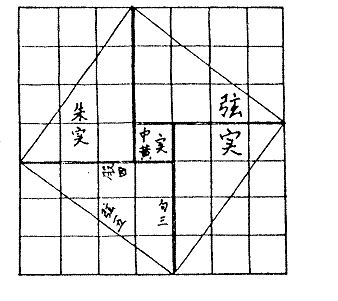Giải trình trên tìm thấy trong bộ sách Chu bễ toán kinh (Zhoubi suànjing) đời Hán. Vì trong hình vẽ, tam giác vuông có ba cạnh chiều dài 3, 4 và 5, nên nhiều nhà nghiên cứu cho rằng thời đó người Trung Quốc chỉ biết trường hợp cá biệt này. Tuy nhiên, một tác giả Trung Quốc thế kỷ thứ III, Triệu Quân Khanh (Zhào Junqing), đã ghi chú hình này và rõ ràng đã chứng minh định lý Pythagore một cách tổng quát (xem J. HOE, Les systèmes d’équations polynômes dans le Siyuan Yujian, Collège de France et I.H.E.C, Paris 1977).