Sur la matière – I
Tout ce que vous
avez toujours
voulu savoir sur la matière sans
oser le
demander – Part-I
Nguyễn Quang
DienDan :
Ce
long texte comportant 6 chapitres sera publié en trois parties,
de deux chapitres chaque, simultanément avec sa traduction
en
Vietnamien.
Il est venu, il est bien là… Qui, quoi ? Le boson nouveau ! Le boson BEHGHK ( Brout-Englert-Higgs-Guralnik-Hagen-Kibble, en abrégé BEH) pour les scientifiques, celui de Higgs pour les profanes, pour les médias la «particule de Dieu»(1). Près de cinquante ans après sa première apparition entre deux lignes d’une équation, au terme d’une traque inédite dans l’histoire scientifique, la Baleine Blanche de la physique des particules s’était enfin fait harponner l’an dernier par le «grand collisionneur de hadrons» (LHC) du CERN : le 4 juillet 2012, après 3.1014 collisions en 2012, au rythme de près d’un milliard par seconde au pic de l’exploitation, les deux équipes Atlas et CMS travaillant indépendamment et en parallèle sur le projet annonçaient la découverte d’une nouvelle particule de masse comprise entre 125 et 127 GeV et dont la «signature» devait être celle du BEH à 5,0 sigma près, c’est-à-dire 5 déviations standard pour chacune des expériences, soit une probabilité de seulement 3 sur 10 million pour que le signal puisse provenir d’une fluctuation statistique du bruit de fond. Mais, tant les enjeux étaient énormes – 10 milliards d’euros d’investissements, un accélérateur circulaire de 27 km de diamètre, 3000 scientifiques et techniciens pour chacune des deux équipes – il a fallu attendre encore plus d’un an pour qu’enfin soit actée la fin de la quête : 5,0 sigma valent bien un prix !(2) Tout en reconnaissant l’apport technique collectif du CERN, le comité Nobel a fait le choix de distinguer Englert et Higgs (Brout étant décédé en 2011), deux des géniteurs théoriques d’un boson fondamental «sans lequel nous n’existerions pas», parce qu’il donne leur masse à d’autres particules élémentaires.
Sans verser dans le mysticisme médiatique sur la «particule de Dieu», on ne peut pas ne pas s’interroger sur le sens de cette phrase cryptique, et le sens même des mots. Qu’est-ce qu’un boson ? Qu’est-ce qu’une particule, élémentaire ou non ? Qu’est-ce que la masse ? Bref, à la fin des fins (ou au commencement des commencements), qu’est-ce que la matière ? La poursuite du BEH a beau s’apparenter à un «polar», il s’agit d’un polar scientifique, qui se doit se lire de A à Z sans pouvoir sauter aucune des lettres intermédiaires. Ou plutôt, le lecteur peut toujours aller directement à Z pour connaître le fin mot de l’histoire, mais alors il ne comprendrait pas tous les termes du dénouement.
La physique des particules de A (les balbutiements de la théorie atomiste) jusqu’à Z (le Modèle Standard de la théorie quantique des champs) ? Mission impossible a priori, tant la science contemporaine s’est éloignée du profane, au point même que son langage lui est devenu inintelligible. Mais nous faisons ici le pari qu’une vulgarisation non outrancièrement simplificatrice reste faisable, qui consisterait à délinéer les idées fondamentales derrière le jargon, à dégager les principes unificateurs derrière la technicité, au prix bien entendu de certaines approximations, omissions ou erreurs que les experts voudront bien nous pardonner, ou de certaines «boîtes noires» (ou plutôt boîtes grises)(3) que les non experts voudront bien accepter sans renoncer à une compréhension globale. L’exposé qui va suivre doit beaucoup à Wikipédia pour la documentation, mais aussi au livre [CTS] pour la technique .

Fig.0 : Simulation de la désintégration du
boson BEH
en quatre
muons (traces jaunes)
1-De l’atome insécable à l’atome de la thermodynamique
Il y a 2500 ans, à une époque où la science était indissociable de la philosophie, les penseurs grecs cherchaient déjà à expliquer les phénomènes naturels de façon rationnelle et unifiée. Leurs spéculations n’avaient bien sûr pas de valeur scientifique exacte, mais après plusieurs millénaires, leur valeur heuristique demeure intacte. Pour les Grecs, le mot cosmos désignait non seulement l’univers, mais un univers harmonieux, c’est-à-dire ordonné, par opposition au chaos. Dans cet ordonnancement, ils distinguaient clairement la forme apparente de la substance matérielle, mais leurs théories sur la constitution de la matière, faute de science expérimentale, s’appuyaient uniquement sur des considérations abstraites de type philosophique. Ainsi de la doctrine atomiste de Leucippe et de son disciple Démocrite (5ème et 4ème siècles av. J-C) : un corps matériel ne peut pas être divisible à l’infini car, s’il l’était, au bout d’une infinité de divisions il ne resterait rien sinon le vide, qui est le contraire de la matière ; il s’ensuit que seule une suite finie de divisions est possible, au bout de laquelle on tombe sur les particules constituantes insécables (atomos) de la matière ; ce sont donc la combinaison des atomes entre eux et leur agencement qui sont à l’origine de tous les agrégats matériels sous leurs différentes formes. Quant aux atomes eux-mêmes, outre leur insécabilité (donc leur inaltérabilité), Démocrite leur attribuait des caractères tels que lisses, rugueux, crochus, ronds, recourbés, etc. censés expliquer les différentes propriétés des composés matériels.
Plus tard, pour expliquer la combinaison des atomes tombant dans le vide, Epicure (4ème siècle av. J-C) devait ajouter le concept de déclinaison, ou clinamen, une déviation spontanée de la verticale, spatialement et temporellement indéterminée, qui permet aux corpuscules, en s’entrechoquant, de se regrouper et s’agréger. Cette conception étonnamment moderne du cosmos interprété comme une cohabitation du vide, de la matière (atomos) et du hasard (clinamen) a été léguée à la postérité surtout à travers le grand poème latin de Lucrèce (1er siècle av. J-C), De natura rerum (De la nature des choses). « Dans le vide tombent éternellement des atomes indivisibles, indestructibles, semences de tous les univers passés, présents ou à venir, car rien ne se crée, rien ne se perd (…) Rien n’est jamais créé divinement de rien. Rien ne s’anéantit ; toute chose retourne, par division, aux corps premiers de la matière » (Livre 1). C’est exprès que nous citons ce passage de Lucrèce, pour bien montrer que bien avant la naissance de la chimie moderne (Lavoisier, 1743-1794) les penseurs grecs se posaient le problème de la (non)création de la matière, et tenaient pour acquis le principe de sa conservation - même si, à y regarder de près, le concept de matière n’est jamais clairement défini. On reviendra plus loin sur les lois de conservation et d’invariance en physique.
Il faut attendre le tournant du 19ème siècle pour voir renaître les thèses atomistes, non plus sous forme spéculative comme chez les anciens Grecs, mais comme une théorie scientifique précise, qualitative et quantitative. Lavoisier avait introduit la notion d’éléments chimiques, ou corps simples (comme l’oxygène, l’hydrogène) qui se combinent pour former tous les composés chimiques existants (comme l’eau), c’est-à-dire les analogues macroscopiques des atomes de Démocrite. Mais c’est John Dalton (1766-1844) qui fait de la théorie atomique la pierre angulaire de la chimie moderne : dans ses recherches de 1803, publiées en 1808, il postule que la matière est constituée d’atomes de masses différentes qui se combinent suivant des proportions simples dont il donne des exemples portant au début sur 6 éléments et 13 combinaisons, par exemple 2H + O donnent H2O, la base même des formules modernes de chimie. L’atomisme revient ainsi sur scène, et il s’impose d’autant plus aisément qu’il se trouve en parfaite concordance avec le nouveau paradigme de la science du 19ème siècle. Ce point mérite un développement (qui n’est pas une digression ; le lecteur de notre polar scientifique ne doit pas sauter cet épisode).
Au tournant du 20ème siècle, les physiciens pouvaient légitimement penser qu’ils approchaient de l’unification ultime rêvée par les penseurs grecs, après l’édification de ces trois monuments synthétiques que sont la mécanique rationnelle née avec Newton (1687) et perfectionnée par Lagrange (1788) et Hamilton (1833) ; l’électrodynamique de Maxwell (1864) ; la thermodynamique théorique, initialisée par Fourier (1811) et parachevée par Maxwell et Boltzmann (autour de 1870).
La mécanique rationnelle en particulier, qui avait permis à partir des concepts fondamentaux de force et de point matériel d’explorer «le cours et les figures des planètes, les chemins de comète, les marées de la mer» (épitaphe de Newton à Westminster Abbey), pouvait nourrir l’ambition d’intégrer les deux autres théories pour rendre compte de l’ensemble des phénomènes physiques observables.
De fait, la moitié de la tâche (une petite moitié, on devait s’en rendre compte au 20ème siècle) était déjà réalisée, grâce à l’hypothèse atomiste, par la thermodynamique statistique de Maxwell-Boltzmann. En rupture avec le déterminisme absolu de l’époque, cette théorie utilise les méthodes statistiques pour connecter les concepts de la mécanique (masse, force) à ceux de la thermodynamique (chaleur, pression, température), permettant ainsi de retrouver et préciser les deux principes fondamentaux énoncés par Carnot (1824). Le premier principe, celui de la conservation de l’énergie, est la traduction macroscopique des lois microscopiques (mécaniques) gouvernant les collisions élastiques des molécules. Le second principe avait été reformulé en 1850 par Clausius en termes d’évolution grâce à la fonction entropie qui mesure «l’état de désordre» d’un système. Une interprétation concrète du second principe se traduit par l’impossibilité d’un mouvement perpétuel qui résulterait de la production de travail à partir d’une seule source de chaleur.
|
La thermodynamique statistique donne une interprétation mécanistique précise de l’entropie S d’un système, définie comme l’intégrale de dq/T, où T est la température et dq la variation de la quantité de chaleur : d’une part, la température, traduite en termes d’agitation moléculaire, est proportionnelle à l’énergie cinétique moyenne des molécules, le facteur de proportionnalité k étant appelé la constante de Boltzmann ; d’autre part, k apparaît également comme un facteur de proportionnalité entre l’entropie S et le logarithme du nombre W de configurations microscopiques dont résulte un état macroscopique donné (on reviendra dans la section 3 sur la notion de «configuration» à propos de la théorie des champs). L’équation de Boltzmann – qui est gravée sur sa pierre tombale au Zentralfriedhof de Vienne – s’écrit ainsi S = k.LogW et donne une mesure exacte du désordre d’un système (plus le nombre de configurations est élevé, plus grand est le désordre), qui doit, suivant le second principe, s’accroître avec le temps si ce système est isolé (voir [CTS] p.53)) |
A l’aube du 20ème siècle, Gibbs (1902), puis Einstein (1905), mettent un point d’orgue à la thermodynamique statistique en y introduisant des concepts probabilistes (par opposition à statistiques) pour pouvoir accéder aux états microscopiques (par opposition à l’état macroscopique) d’un système physique : la probabilité d’un micro-état d’un système à l’équilibre est reliée par Einstein au temps moyen que le système passe dans ce micro-état dans un intervalle de temps tendant vers l’infini, ce qui lui permet d’élaborer une théorie à la fois qualitative et quantitative du mouvement brownien (mouvement aléatoire d’une «grosse» particule plongée dans un fluide et soumise à aucune autre interaction qu’avec les «petites» molécules du fluide) qui fournit à Jean Perrin le cadre de certaines expériences dites «critiques» (en ce sens qu’elles doivent confirmer ou infirmer toute la théorie) qui apportent en 1908 les premières preuves irréfutables de l’existence des atomes, ainsi qu’une idée de leur taille (entre 6.10-10 et 6.10-11 m)(voir [CTS] pp.55-56). Bien sûr, en matière de «preuves» pour l’homme de la rue, on a fait mieux depuis : les premières photos d’atomes de fer ont été prises dans les années 1960, et en mai 2013 , une équipe d’IBM a réussi l’exploit de réaliser, image par image, un clip d’une minute en manipulant quelques dizaines d’atomes de carbone sur une plaque de cuivre (voir fig. 1.1 et 1.2)
 |
 |
|
Fig. 1.1 & 1.2: Les points constituant le personnage sont des atomes de carbone grossis 100 M de fois par un microscope à effet de champ, à une température proche du zéro absolu |
|
2-De l’atome planétaire à l’atome de Bohr
A la fin du 19ème siècle, l’état d’avancement du grand œuvre d’unification de la physique par extension des concepts de base de la mécanique se présente ainsi : l’intégration de la thermodynamique, voire de la chimie, s’est faite en s’appuyant sur l’hypothèse atomiste pour étendre le concept de point matériel ; il reste à connecter la notion de force aux phénomènes électromagnétiques de la théorie de Maxwell, ce qui occupera essentiellement toute la physique théorique du 20ème siècle, et au prix de la restructuration complète de ses fondements. Dans le premier quart du siècle, les crises conceptuelles (et leurs résolution) vont se bousculer à un rythme et avec une simultanéité qui rendent difficile (et d’ailleurs non souhaitable) toute tentative de récit linéaire. On fera plutôt le choix de suivre le développement de certaines idées-force, quitte à faire des allers-retours chronologiques.
Comme on l’a vu, le modèle atomiste s’impose définitivement au tournant du siècle. Mais dès 1879, les travaux de Joseph John Thomson (prix Nobel de physique en 1906) sur les rayons cathodiques le conduisent à la découverte de l’électron, particule chargée négativement (sa charge sera prise comme unité de charge pour les particules atomiques), d’une masse est égale approximativement à 5,5x10-4 celle de l’atome d’hydrogène : atomos n’est plus insécable. Thomson émet l’idée d’électrons plongés dans une masse positive «comme des raisins dans un gâteau», mais en 1911, en bombardant une mince feuille d’or avec des particules alpha (noyaux des atomes d’hélium), Ernest Rutherford (prix Nobel de chimie en 1908) s’aperçoit que la majorité des particules traverse la feuille en subissant une légère déviation, alors que certaines sont rejetées en arrière. Il en conclut que la charge positive de l’atome doit être concentrée dans une petite partie centrale appelée noyau, environ 100.000 fois plus petite que l’atome (qui est donc fait surtout de vide). Rutherford propose le modèle «atomique planétaire» qui porte son nom, des électrons tournant autour d’un noyau central de charge opposée comme des planètes autour d’un soleil.
Reste à affiner la structure du noyau. En 1919, en bombardant avec des alpha un gaz d’azote, Rutherford montre que le noyau d’hydrogène se retrouve dans les noyaux d’autres éléments, donc qu’il doit s’agir d’une particule élémentaire baptisée proton («premier»), dont la charge vaut -1 et la masse environ 1836 fois celle de l’électron (la masse du proton sera prise comme unité de masse pour les particules atomiques). Par ailleurs, à la suite de résultats expérimentaux intrigants sur un rayonnement pris à tort pour une radioactivité gamma (voir plus loin), James Chadwick (prix Nobel de physique en 1935) met en évidence en 1932, en bombardant des atomes de beryllium avec des alpha, l’existence d’une particule de masse 1 et de charge 0, baptisée neutron. Encore aujourd’hui, l’image de l’atome familière au grand public est un modèle planétaire simple (fig. 2.1) : les trois particules élémentaires sont le proton, le neutron et l’électron ; les électrons tournoient sur différentes orbites, dans des couches orbitales plutôt, autour d’un noyau composé de protons et neutrons (appelés pour cela nucléons) ; le numéro atomique Z est le nombre de protons (égal au nombre d’électrons), la masse atomique A est la masse du noyau, c-à-d. la somme des masses des protons et des neutrons.
Mais on doit avouer que cette simplicité confine au simplisme. Certes, le modèle de Rutherford satisfait pratiquement totalement aux besoins de la chimie : les liaisons chimiques se font par combinaisons d’électrons, le numéro atomique «explique» la périodicité du tableau de Mendeleïev (une classification empirique des corps simples en fonction de propriétés périodiques, voir fig. 2.2), la masse atomique «explique» l’existence d’éléments isotopes (éléments ayant même Z, mais des A différentes), etc.
Mais il en va autrement en physique, où le modèle planétaire se révèle à la fois instable et insuffisant. Instable par sa conception même : suivant les lois de Maxwell, des charges électriques en mouvement devraient rayonner, et donc les électrons devraient perdre leur énergie et tomber sur le noyau ; à l’intérieur même du noyau, les protons, ayant des charges de même signe, devraient se repousser mutuellement , etc. Insuffisant car laissant inexpliqués des phénomènes tels que la cohésion d’un noyau agrégé par une mystérieuse «force de liaison» non détectée (et non anodine, on le verra dans la section 3) ; et sa désagrégation par la radioactivité - naturelle (Becquerel, 1896) ou artificielle (les époux Joliot-Curie, 1934) - plus précisément, la transmutation ou la désintégration de certains noyaux atomiques , avec éjection de particules et dégagement de rayonnements (la radioactivité alpha produit de noyaux d’hélium, la bêta des électrons, la gamma , des rayonnements plus pénétrants que les rayons X) en contradiction apparente avec le principe de conservation de l’énergie, etc.
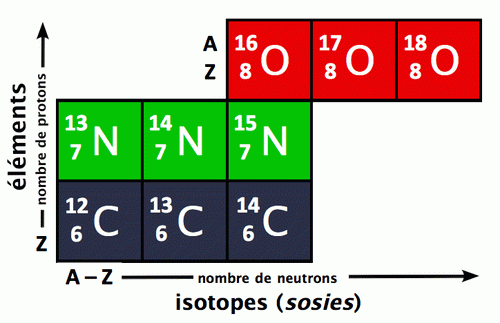
Fig. 2.1 : Tableau périodique des éléments
et les
positions des isotopes

Fig. 2.2 Tableau périodique
De fait, expliquer «la force qui fait vibrer les particules de l’atome et tient ce minuscule système solaire qu’est l’atome en un seul morceau», selon le souhait de Max Planck (et l’on verra qu’il est encore trop naïf), ce sera l’œuvre essentielle de la physique théorique du 20ème siècle, mais pas avant qu’elle ait fait deux fois sa révolution conceptuelle.
En cette fin de siècle, dressant l’état des lieux de la physique théorique en 1900, Lord Kelvin (William Thomson, à ne pas confondre avec J-J.) veut bien concéder qu’il y a encore « deux petits nuages dans le ciel serein » de la physique - la «catastrophe ultraviolette» d’une part, l’absence de «vent d’éther» d’autre part - mais il ne doute pas qu’ils vont rapidement se dissiper. Quelques mois seulement après, éclate le premier nuage.
La révolution quantique
La «catastrophe ultraviolette» est le nom imagé donné à la non concordance entre les résultats théoriques et expérimentaux sur le rayonnement électromagnétique du «corps noir», c-à-d. d’un corps totalement en équilibre thermodynamique avec son milieu. La théorie classique montre que les caractéristiques de ce rayonnement ne dépendent pas du corps, seulement de sa température. Il s’agit alors de décrire, pour une température T donnée, la répartition énergétique spectrale, c-à-d. la densité d’énergie volumique en fonction de la fréquence. Les résultats expérimentaux dessinent une courbe en forme de cloche dissymétrique, plus ou moins aplatie suivant la température (fig. 2.3 et 2.4). La thermodynamique classique en fournit une bonne approximation à basse fréquence (loi de Rayleigh-Jeans), mais à haute fréquence (donc pour les courtes longueurs d’onde), elle prédit absurdement une énergie infinie : c’est la catastrophe UV ! La loi de Planck de 1900 y remédie en donnant l’expression correcte du rayonnement dans une formule frappante qui réunit trois constantes universelles : la vitesse de la lumière c, la constante de Boltzmann k, ainsi qu’une nouvelle constante, h, qui signe l’acte de naissance des théories quantiques. Le qualificatif vient de quantum, qui signifie en latin «quantité élémentaire». Dans son raisonnement, pour pouvoir utiliser la thermodynamique statistique (voir section 1), Planck postule que les échanges d’énergie entre le corps noir et le rayonnement électromagnétique se font de façon discontinue, plus précisément par multiples entiers d’un quantum d’action qu’on notera Epsilon. L’idée d’un échange discontinu d’énergie est un concept totalement révolutionnaire, contraire à la fois à l’intuition et aux présupposés de la physique de l’époque (ce qui explique peut-être pourquoi le prix Nobel de physique ne sera décerné à Planck qu’en 1918).
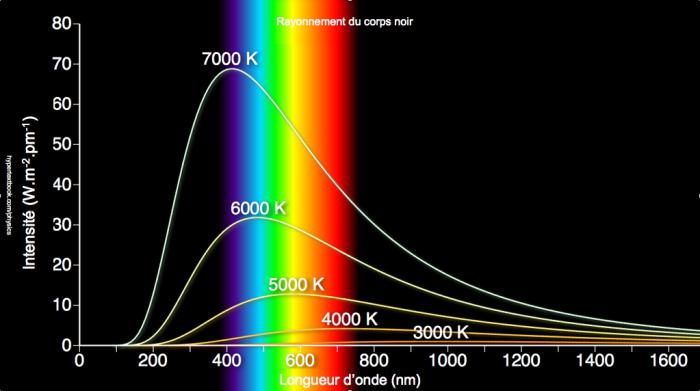
Fig. 2.3 : Le rayonnement du corps noir : résultats expérimentaux
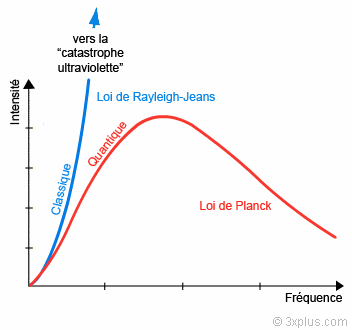
Fig. 2.4 : Le rayonnement du corps noir : Modèles théoriques
|
Pour calculer Epsilon, Planck évalue de deux façons différentes l’entropie du corps noir, utilisant d’un côté les propriétés thermodynamiques classiquement connues de l’interaction du rayonnement électromagnétique avec la matière, de l’autre la description statistique de l’entropie de Boltzmann. Pour que ces deux approches soient compatibles, Planck doit postuler que Epsilon est proportionnel à la fréquence Nu du rayonnement, ce qui s’écrit Epsilon = h.Nu , où h est la constante universelle de Planck, qui a donc la dimension d’une énergie multipliée par un temps (voir [CTS] p. 107). Compte tenu de cette quantification, la statistique de Boltzmann montre qu’un état vibratoire porte en moyenne l’énergie h.Nu/exp(h.Nu/kT)-1 ; le produit par la densité d’états vibratoires possibles donne la «densité d’énergie de Planck», qui décrit correctement le rayonnement du corps noir à la température T. |
Désormais, on qualifiera de «quantique» tout phénomène, toute théorie où interviendra - directement ou indirectement - la constante de Planck. Même un profane devrait sentir à ce stade que la «discrétisation» (quantification) par Planck du concept d’énergie est un premier pas vers l’unification de l’électromagnétisme et de la mécanique évoquée depuis le début.
En 1905, «l’année miraculeuse» où il publie sa théorie de la relativité restreinte et sa théorie du mouvement brownien, Einstein se saisit de l’idée quantique pour interpréter l’effet photoélectrique, c’est-à-dire la production d’un courant d’électrons quand un rayonnement frappe un corps photoélectrique (par exemple des électrodes immergées dans un liquide, dans l’expérience des Becquerel en 1839) : l’effet ne se produit qu’au-dessus d’un certain seuil de fréquence du rayonnement, et au-dessus de ce seuil, l’énergie des électrons produits ne dépend pas de l’intensité du rayonnement. Ce phénomène est inexplicable en s’en tenant à la seule nature ondulatoire du rayonnement. Il devient clair par quantification : l’énergie du rayonnement étant communiquée à la substance photoélectrique par quanta d’action, le seuil de fréquence n’est autre qu’un seuil d’énergie qui correspond à l’énergie de liaison de l’électron avec l’atome, et l’énergie communiquée à l’électron, une fois arraché, ne dépend plus de l’intensité du rayonnement frappant la substance (voir [CTS] p.109). Einstein réintroduit ainsi à sa manière la conception corpusculaire de la lumière défendue par Newton, mais on verra plus loin que le «grain de lumière» newtonien, remplacé par le quantum d’action de lumière appelé photon, est une «particule sans masse», parce qu’il se déplace à la vitesse de la lumière. Einstein se verra attribuer le prix Nobel en 1921 pour son explication de l’effet photoélectrique (et pas pour la théorie de la relativité, contrairement à une croyance répandue).
En 1913, dans le sillage de Planck et d’Einstein, Niels Bohr (prix Nobel en 1922) quantifie le modèle planétaire de l’atome en posant deux principes :
-
un électron ne peut se déplacer que sur un certain nombre d’orbites stables, bien différenciées (quantification des orbites)
-
l’électron sur une orbite stable ne rayonne pas. Il ne rayonne ou n’absorbe de l’énergie qu’en changeant d’orbite (transition électronique)
|
Bohr détermine les orbites par un calcul d’énergie combinant les principes classiques et quantiques. Prenons l’exemple de l’atome d’hydrogène, où un seul électron de masse m tourne autour d’un seul proton sur une orbite circulaire de rayon r , à une vitesse v . Les expressions classiques de la force d’attraction électrostatique (Coulomb) et de l’énergie cinétique d’un point matériel soumis à une force centrale (Newton) conduisent à l’équation mv2 = re2, où, par commodité, e désigne la charge électrique divisée par une constante reliée à la «permittivité» du vide. Mais dans la théorie cinétique d’un point matériel M en mouvement par rapport à un point fixe O, intervient aussi le moment cinétique, qui est un vecteur L égal au produit vectoriel de OM par p, où p = mv est le vecteur quantité de mouvement (on écrit les vecteurs en caractères gras, leur longueur en caractères ordinaires ; ainsi v est le vecteur vitesse, dont la longueur est la vitesse scalaire v). Dans le mouvement circulaire étudié ici, L = mrv. Le premier principe de Bohr s’énonce précisément sous la forme L = n.ћ, où ћ est la constante de Planck normalisée en divisant h par 2π, donc mrv = n.ћ , où n est un nombre entier (n = 1, 2, 3,…). En rapprochant les deux expressions obtenues pour la vitesse, on trouve que les rayons et les énergies des orbites possibles s’ordonnent en deux suites : rn = an2,où a = ћ2/me2 est le «rayon de Bohr», et En = E1/n2, où E1 = me4/2ћ est l’énergie de la plus basse couche. La quantification des orbites correspond ainsi à une quantification de niveaux d’énergie, et le second principe de Bohr exprime que les quanta d’énergie échangés par l’électron se présentent sous la forme E1(1/n2 – 1/n’2), où n et n’ sont des entiers. |
La confirmation expérimentale est immédiate, les résultats se trouvaient par avance dans l’analyse spectrographique d’un gaz chauffé à basse pression : d’après la relation de Planck, la quantification des niveaux d’énergie doit se traduire par une quantification des longueurs d’onde du rayonnement de l’électron, et c’est bien ce qu’on observe par exemple dans le spectre de l’hydrogène, qui présente des raies spectrales espacées comme le prédit la formule de Bohr (voir fig. 2.4). Certes le modèle de Bohr ne pouvait tout expliquer, ni certaines petites irrégularités dans le tableau de Mendeleïev, ni la structure fine des raies spectrales de l’hydrogène (qui se dédoublent en deux raies très proches), ni l’expérience de Stern-Gerlach (un faisceau d’atomes d’argent dans un champ magnétique vertical non uniforme se sépare en deux)…
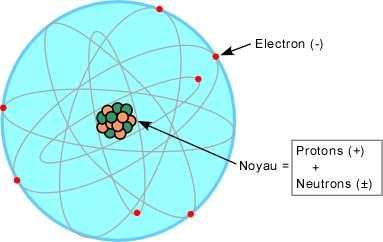
Fig. 2.5 : Modèle atomique de Rutherford
Mais même si ce n’est que le premier balbutiement de la future mécanique, la quantification des orbites électroniques permet de lever le paradoxe de leur stabilité. Grâce au concept lié de seuil d’énergie (déjà exploité par Einstein), elle permet même de résoudre un autre paradoxe, celui de la permanence des atomes, qui donnait des angoisses métaphysiques à Maxwell quand il s’interrogeait sur des particules qui «à travers tout l’univers, portent imprimé en elles le sceau d’un système métrique aussi distinctivement que le mètre des archives à Paris [et dont] l’égalité exacte de chacune à toutes les autres de même type leur donne le caractère essentiel des articles manufacturés» : de fait, tant que les perturbations énergétiques restent inférieures à un certain seuil, l’atome demeure indivisible au sens étymologique du terme.
Oui mais, nous dira-t-on, et l’instabilité et la désintégration de certains noyaux ? La réponse est à chercher dans l’autre révolution scientifique du 20ème siècle, la théorie de la relativité.
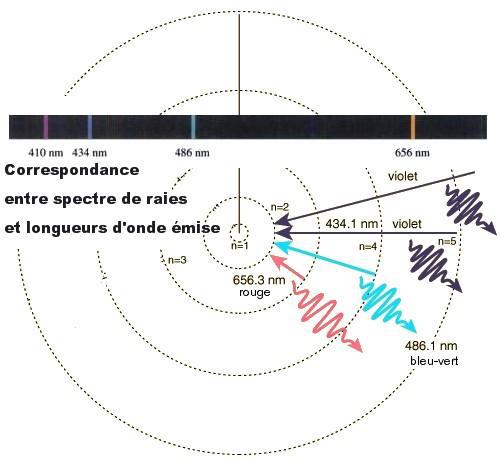
Fig. 2.6 : Modèle atomique de Bohr
Nguyễn Quang
(1) Interprétation déformée (volontairement ?) d’une exclamation du physicien Leon Lederman, «that Goddamn particle!»
(2) Fin 2011, une équipe de physiciens travaillant sur le projet OPERA annonça prématurément avoir détecté des neutrinos voyageant plus vite que la lumière. Quand il fallut reconnaître qu’il s’agissait d’une erreur due à une fibre optique défaillante, plusieurs membres prestigieux d’OPERA se crurent obligés de démissionner
(3) Ce sont des paragraphes écrits dans un cadre teinté en gris.
Bibliographie
[B] J. Baggott : La particule de Dieu – A la découverte du boson de Higgs, Dunod, 2013
[CTS] G. Cohen-Tannoudji & M. Spiro : Le boson et le chapeau mexicain – Un nouveau grand récit de l’Univers, Folio Essais, 2013
[GV] C. Grojean & L. Vacavant : A la recherche du boson de Higgs, Librio 2013
Attention - Le niveau de ces trois références n’est pas le même : [GV] s’apparente à un article pour grand public ; [B] se concentre sur l’aspect historique ; la technicité de [CTS] n’en fait pas un livre pour profanes débutants.
Các thao tác trên Tài liệu










