Về vật chất – I
Tất cả
những gì bạn vẫn muốn
biết từ
lâu về vật chất,
nhưng còn
ngại hỏi – Phần-I
Nguyễn Quang
Diễn Đàn :
Bài này gồm 6 chương, vì khá
dài nên chúng tôi chia làm ba
phần, mỗi phần hai chương, xuất bản cùng
với nguyên
tác bằng tiếng Pháp.
Tới rồi, có đây... Cái gì thế ? ai đó vậy ? Thưa, hạt boson mới ! Boson BEHGHK (tên tắt của Brout-Englert-Higgs-Guralnik-Hagen-Kibble, viết gọn lại thành BEH) theo các nhà khoa học, người bình thường dùng tên boson Higgs, và với truyền thông thì nó còn là "hạt của chúa"(1). Trước đây gần 50 năm, nó thấp thoáng hiện ra lần đầu giữa mấy dòng phương trình, và từ đó là một cuộc săn tìm vô song trong lịch sử khoa học, cho tới khi cuối cùng con "cá voi trắng" quý hiếm này đã bị đánh bắt vào năm ngoái trong "máy gia tốc hạt hadron vĩ đại" LHC của tổ chức CERN : Sau 3*1014 va chạm trong năm 2012, với nhịp độ đỉnh là gần 1 tỷ lần mỗi giây, ngày 04.07.2012, hai nhóm nghiên cứu Atlas và CMS, vốn làm việc song song và độc lập với nhau trên chương trình này, đã loan báo sự phát hiện một hạt cơ bản mới, có khốí lượng trong khoảng giữa 125 và 127 GeV, mang "dấu ấn" của hạt BEH một cách chắc chắn với độ tin cậy 5,0 sigma, có nghĩa là tín hiệu chỉ có xác suất 3 phần 10 triệu là do đến từ nhiễu nền, theo thống kê. Nhưng, bởi vì cái-được-thua lớn khủng khiếp – đầu tư 10 tỷ Euros cho một máy gia tốc hạt hình tròn chu vi 27 km, hai nhóm nghiên cứu mỗi nhóm có 3000 nhà khoa học làm việc – người ta đã phải đợi thêm hơn một năm, cuối cùng mới chứng thực là cuộc săn tìm đã kết thúc : 5 sigma đúng là có cái giá của nó !(2) Tuy một mặt vẫn công nhận đóng góp kỹ thuật của tập thể CERN, ủy ban Nobel đã chọn lựa vinh danh Englert và Higgs (Brout đã qua đời năm 2011), hai người "cha" của lý thuyết về một boson cơ bản mà "nếu không có nó chúng ta cũng không thể hiện hữu", bởi vì chính nó đem lại khối lượng cho những hạt cơ bản khác.
Boson là cái gì ? một hạt, cơ bản hay không, là cái gì ? khối lượng là gì ? Tóm lại, đến tột cùng (hay là ở khởi đầu của mọi khởi đầu), vật chất là cái gì ? Không rơi vào cái thần bí truyền thông về "hạt của chúa", người ta cũng không thể không tự hỏi về ý nghĩa của câu văn bí hiểm trên, và cả về ý nghĩa của từng chữ trong đó. Cuộc săn tìm BEH tuy có vẻ như một truyện "trinh thám", nhưng đây là một truyện trinh thám khoa học, phải được đọc từ A đến Z mà không thể nhảy cóc qua một chữ cái nào. Hay đúng hơn, độc giả vẫn có thể nhảy đến ngay chữ Z để biết câu chuyện sẽ kết thúc ra sao, nhưng khi đó bạn sẽ không thể hiểu tất cả những tình tiết của màn chung cục.
Vật lý lượng tử, nói từ A (thuyết nguyên tử sơ khai) đến Z (Mô hình chuẩn của thuyết trường lượng tử) ? Tiên thiên là nhiệm vụ bất khả, bởi vì khoa học đương đại đã đi quá xa người ngoại đạo, đến nỗi anh ta không thể hiểu ngôn ngữ của nó. Nhưng ở đây chúng tôi chấp nhận đánh cuộc rằng có thể thực hiện một sự phổ biến khoa học mà không giản lược quá thô bạo, bằng cách phác hoạ những ý tưởng nền tảng nằm ở đằng sau ngôn ngữ chuyên môn ; dĩ nhiên với cái giá phải trả bằng một số điều chỉ nói được gần đúng, một số điều bị lược bỏ hay sai lầm mà xin được các chuyên gia tha thứ, hay bằng những "hộp đen" (đúng hơn, hộp xám)(3) mà xin được người ngoại đạo chấp nhận để không từ bỏ tầm hiểu biết tổng quát. Bài này mang nợ rất nhiều từ Wikipedia về mặt tài liệu, và từ tác phẩm [CTS] về mặt kỹ thuật.

Hình-0 : Mô phỏng sự phân rã của boson BEH thành 4 muons (các vết màu vàng)
I. Từ nguyên tử bất khả phân đến nguyên tử nhiệt động học
2500 năm trước,
trong thời mà khoa học không thể tách
khỏi triết học, các nhà tư tưởng
Hy Lạp đã tìm cách giải thích
các hiện tượng tự nhiên một
cách thuần lý và thống nhất.
Những tư biện của họ đương
nhiên không có giá trị khoa học
chính xác, nhưng trải qua nhiều thế
kỷ, chúng vẫn mang nguyên vẹn những
giá trị khai phá. Danh từ cosmos,
đối với người Hy Lạp, không
chỉ có nghĩa là "vũ trụ",
mà còn là một vũ trụ hài
hoà, trong nghĩa có trật tự, đối
lập với chaos, cái hỗn loạn
nguyên thuỷ. Trong trật tự đó, họ
phân định được rõ ràng
hình thể hiển hiện của vật chất,
nhưng những lý thuyết của họ về
sự cấu tạo của vật chất, do thiếu
vắng khoa học thực nghiệm, chỉ dựa
vào những suy luận trừu tượng
kiểu triết học. Nguyên tử luận
của Leucippe và môn đệ Démocrite
(thế kỷ thứ 5 và thứ 4 trước
C.N.) là như thế : Một khối vật
chất không thể bị chia nhỏ mãi
đến vô tận, vì nếu làm
được thì sau đó sẽ không
còn gì, chỉ còn chân không,
cái ngược lại của vật chất ;
từ đó suy ra, chỉ có thể lập
lại một số lần có giới hạn
việc chia nhỏ vật chất, sau đó
kết quả là một tổng thể những
hạt bất khả phân (nguyên nghĩa của
atomos, nguyên tử), làm thành vật
chất ; vậy thì chính là do sự
kết tập các nguyên tử và tổ
chức giữa các nguyên tử với nhau
mà hình thành nên tất cả những
hình thái khác nhau của vật chất.
Còn về bản thân các nguyên tử,
ngoài tính bất khả phân (và do
đó chúng cũng bất biến),
Démocrite còn gán cho chúng những
đặc dạng như: nhẵn nhụi, sần
sùi, tròn, méo, có móc... có
khả năng giải thích các tính
chất khác nhau của các phức hợp
vật chất.
Sau này, để giải thích tại sao các nguyên tử, đang cùng rơi trong khoảng không, lại kết tập được với nhau, Epicure (thế kỷ thứ 4 trước C.N.) đã đưa ra khái niệm clinamen (rẽ nghiêng), một hạt nhỏ có thể di chuyển ra ngoài quỹ đạo rơi thẳng đứng, một cách bất chợt và bất kỳ. Điều này khiến cho các nguyên tử có thể va chạm và kết dính với nhau. Thật hiện đại đáng ngạc nhiên, quan niệm về cosmos này diễn tả vũ trụ như nơi mà chân không, vật chất (atomos), và cái ngẫu nhiên (clinamen) cùng chung sống. Hậu thế được thừa hưởng quan niệm đó chủ yếu qua thi phẩm Latinh vĩ đại của Lucrèce (thế kỷ thứ nhất trước CN), De natura rerum (Về bản chất của vạn vật). "Trong chân không vĩnh viễn rơi những nguyên tử bất khả phân, bất khả diệt, mầm mống của cả vũ trụ trong quá khứ, hiện tại và vị lai, bởi vì không có gì tự nhiên phát sinh, không có gì biến mất (...) Không có gì được thần linh sáng tạo từ hư vô. Không có gì sẽ biến thành hư vô ; cái gì cũng phân rã trở lại thành những thành phần đầu tiên của vật chất" (Quyển I). Chúng tôi cố ý trích dẫn đoạn thơ trên của Lucrèce, để cho thấy rằng, rất lâu trước khi nền Hoá học hiện đại được khai sinh (Lavoisier, 1743-1794), các nhà tư tưởng Hy Lạp đã đặt ra vấn đề (không-)phát-sinh vật chất, và coi nguyên lý bảo tồn vật chất như là chuyện đã rõ – mặc dù, nếu soi kỹ, khái niệm vật chất chẳng hề được xác định rõ ràng. Chúng ta sẽ trở lại ở một đoạn sau với những quy luật bảo tồn và bất biến trong vật lý.
Phải đợi khúc ngoặt sang thế kỷ 19 người ta mới thấy xuất hiện trở lại các luận đề về nguyên tử, không còn dưới dạng tư biện nữa, mà như một lý thuyết khoa học chính xác trên cả hai mặt định tính và định lượng. Lavoisier đã mang đến khái niệm chất hoá học đơn, đơn chất hay nguyên tố (như hyđrô, ôxy), chúng kết hợp với nhau để hình thành tất cả những chất hoá học phức hợp (hợp chất) hiện hữu (thí dụ như nước), hiện tượng vĩ mô tương tự như với các nguyên tử vi mô của Démocrite. Nhưng chính John Dalton (1766-1844) là người đặt lý thuyết nguyên tử ở tầng nền tảng của hoá học hiện đại : trong những nghiên cứu vào năm 1803, công bố năm 1808, ông đặt định đề là vật chất được cấu tạo bởi những nguyên tử có khối lượng khác nhau, và chúng kết hợp với nhau theo những tỷ lệ đơn giản. Bước đầu ông đưa ra 13 tổ hợp, dùng 6 đơn chất, thí dụ như 2H + O sẽ cho ra H2O, ký hiệu khởi thuỷ của các công thức hoá học. Và thế là thuyết nguyên tử trở lại sân khấu, và nó càng dễ dàng chiếm vai chính hơn khi rất thích hợp với hệ hình (paradigme) mới của khoa học thế kỷ 19. Điểm này cần được phát triển thêm (không phải để vẽ rắn thêm chân, bạn đang đọc một truyện trinh thám khoa học, xin đừng nhảy qua mắt xích dưới đây).
Tới khúc ngoặt sang thế kỷ 20, các nhà vật lý có cơ sở xứng đáng để nghĩ rằng họ đang tiến gần đến sự thống nhất tối hậu mà các nhà tư tưởng Hy Lạp từng ước mơ ; sau khi ba công trình tổng hợp lớn đã được xây dựng, đó là : cơ học thuần lý do Newton (1687) khai sinh và được Lagrange (1788) cũng như Hamilton (1833) hoàn thiện, điện từ học của Maxwell (1864), lý thuyết nhiệt động học, do Fourier (1811) khai sáng rồi được Maxwell và Boltzmann (vào khoảng 1870) hoàn chỉnh.
Nói riêng về cơ học thuần lý, khởi đi từ những khái niệm cơ bản về lực và điểm vật chất, nó cho phép khảo sát " cấu hình và sự biến chuyển của các hành tinh, quỹ đạo của sao chổi, thuỷ triều" (ghi trên bia mộ Newton ở Westminster Abbey). Vậy người ta cũng có thể mang tham vọng tích hợp được nó với hai lý thuyết kia để từ đó giải thích tất cả những hiện tượng vật lý quan sát được.
Thực ra, nhờ vào giả thuyết nguyên tử, nhiệm vụ ấy đã hoàn thành một nửa (nửa nhỏ thôi, như người ta sẽ thấy ra trong thế kỷ 20), qua nhiệt động học thống kê của Maxwell-Boltzmann. Đoạn tuyệt với quan điểm tất định tuyệt đối đương đại, lý thuyết này sử dụng những phương pháp thống kê để nối liền những khái niệm cơ học (lực và khối lượng) với những khái niệm của nhiệt động học (nhiệt năng, nhiệt độ, áp suất), bằng cách ấy tìm lại được và đồng thời xác định rõ hơn hai nguyên lý cơ bản của nhiệt động học mà Carnot đã phát biểu. Nguyên lý thứ nhất, nguyên lý bảo tồn năng lượng, là sự diễn dịch vĩ mô của các quy luật ở tầm vi mô về va chạm cơ học đàn hồi của các phân tử. Nguyên lý thứ hai, đã được Clausius phát biểu lại năm 1850, dưới dạng biến thiên của hàm entropy (biểu diễn "trạng thái mất trật tự" của một hệ thống, không thể giảm trong một hệ cô lập). Một diễn dịch cụ thể của nguyên lý thứ hai nói rằng không thể có chuyển động vĩnh cửu, vì như thế cuối cùng có thể sinh ra tác dụng trong một môi trường chỉ có một nguồn nhiệt.
|
Nhiệt động học thống kê giải thích khái niệm entropy một cách chính xác bằng cơ học. Entropy S của một hệ thống được định nghĩa như tích phân của dq/T, trong đó T là nhiệt độ, và dq là biến thiên của nhiệt lượng : Một mặt thì nhiệt độ, diễn tả sự dao động của các phân tử, là tỷ lệ với động năng trung bình của các phân tử, hệ số tỷ lệ k được gọi là hằng số Boltzmann ; mặt khác, k còn hiện ra như một hệ số tỷ lệ giữa entropy S và lôgarít của W, số các cấu hình vi mô của một trạng thái vĩ mô nhất định (chúng ta sẽ trở lại khái niệm cấu hình trong chương 3 khi bàn về lý thuyết trường). Do đó phương trình Bolzmann – được khắc trên bia mộ của ông tại Zentralfriedhof ở Vienne – được viết như sau : S = k.LogW, và cho ra một định lượng chính xác về độ hỗn loạn của một hệ thống (con số cấu hình càng cao thì độ hỗn loạn càng lớn). Theo nguyên lý thứ hai thì S chỉ có thể tăng theo thời gian, nếu hệ thống đó cô lập (xem [CTS] tr.53)) |
Khi thế kỷ 20 rạng sáng, Gibbs (1902), rồi Einstein (1905), đã đặt một dấu lặng cho nhiệt động học thống kê khi đưa vào sử dụng những khái niệm của toán học xác suất (đối lập với thống kê) để có thể khảo sát những trạng thái vi mô (đối lập với vĩ mô) của một hệ thống vật lý : xác suất hiện ra một trạng thái vi mô nhất định của một hệ thống được Einstein liên hệ với quãng thời gian trung bình mà hệ thống nằm trong trạng thái vi mô đó trong một khoảng thời gian tiến đến vô tận. Địều này cho phép Einstein xây dựng một lý thuyết vừa định tính vừa định lượng về chuyển động Brown (chuyển động ngẫu nhiên của một vi hạt "lớn" nằm trong một chất lỏng, và không chịu bất cứ một tác động nào khác ngoài sự va chạm với các phân tử của chất lỏng ấy). Thành quả này tạo khung cảnh cho Jean Perrin thiết kế một số thí nghiệm có tính "quyết định" (theo nghĩa nó cho phép phán định toàn bộ một lý thuyết là đúng hay sai) ; và đem lại vào năm 1908 những bằng chứng không thể chối cãi đầu tiên về sự hiện hữu của các nguyên tử, cũng như một ước lượng về độ lớn của chúng (giữa 6.10-10 và 6.10-11 m) (xem[CTS] tr.55-56). Và đương nhiên, về "bằng chứng" cho người bình thường thì từ đó người ta đã trưng ra nhiều thứ hay hơn : nguyên tử sắt đã được chụp ảnh trong những năm 1960, và vào tháng 5.2013, một nhóm nghiên cứu của IBM đã thực hiện một kỳ công là công bố một phút phim hình chiếu trong đó, mỗi hình được vẽ bằng vài chục điểm nguyên tử đặt trên một miếng đồng (xem Hình 1.1 và 1.2).
 |
 |
|
Hình 1.1 và 1.2: Mỗi điểm dùng vẽ ra cậu bé này là một nguyên tử các-bon được phóng to 100 triệu lần bằng kính hiển vi dùng hiệu ứng đường hầm, trong nhiệt độ gần độ không tuyệt đối. |
|
2. Nguyên tử hành tinh và nguyên tử kiểu Bohr
Về cuối thế kỷ 19, tình trạng tiến triển của sự nghiệp vĩ đại đi tìm cái thống nhất của vật lý, bằng cách mở rộng những khái niệm nền tảng của cơ học, là như sau : Sự tích hợp với nhiệt động học, ngay cả với hoá học nữa, đã thành công khi dựa trên giả thuyết nguyên tử để mở rộng khái niệm điểm vật chất ; điều còn lại là liên kết khái niệm lực với các hiện tượng điện từ trong lý thuyết của Maxwell, đó chủ yếu là sự bận rộn của tất cả hoạt động vật lý lý thuyết của thế kỷ 20, và với cái giá là phải cấu trúc lại toàn bộ nền tảng vật lý học. Trong một phần tư thế kỷ đầu, những khủng hoảng về khái niệm (và các giải pháp) xô đẩy nhau, chồng chất lên nhau, theo một nhịp điệu khiến cho khó có thể (vả lại cũng không nên) kể một câu chuyện theo thời gian tuyến tính. Thay vì thế, chọn lựa ở đây là lần bước theo sự phát triển của một vài ý tưởng chủ đạo, và nếu cần thì sẵn sàng ngược xuôi với thời gian.
Như chúng ta thấy, mô hình nguyên tử đã bền vững ngự trị từ khúc quanh đi vào thế kỷ. Nhưng, ngay từ 1879, những nghiên cứu của Joseph John Thomson (giải Nobel de vật lý năm 1906) về tia điện cực âm (tia catôt) đã đưa ông đến sự khám phá ra điện tử, hạt cơ bản mang điện tích âm (điện tích này sẽ được quy định là đơn vị điện tích cho những vi hạt nguyên tử) và có khối lượng bằng 5,5x10-4 khối lượng của nguyên tử Hydrô : atomos không phải là bất khả phân nữa rồi. Thomson gợi ý là các điện tử nằm chìm trong một thể chất mang điện tích dương, "như các hạt nho khô nằm trong cái bánh", nhưng đến năm 1911, khi bắn vào một lá vàng mỏng bằng một chùm tia alpha (lõi của các nguyên tử hêlium) Ernest Rutherford (giải Nobel hoá học năm 1908) nhận ra rằng đa số các vi hạt alpha xuyên qua lá vàng và bị lệch hướng nhẹ, trong khi có một số nhỏ vi hạt bị bắn ngược trở lại. Từ đó ông đi đến kết luận là điện tích dương của nguyên tử phải được tập trung trong một phần trung tâm rất nhỏ của nó, đặt tên là lõi nguyên tử, nhỏ hơn nguyên tử khoảng 100.000 lần (tuyệt đại bộ phận nguyên tử là chân không). Rutherford đề nghị mô hình "nguyên tử hành tinh" mang tên ông, theo đó các điện tử quay chung quanh một cái lõi có điện tích ngược lại, như các hành tinh quay chung quanh mặt trời.
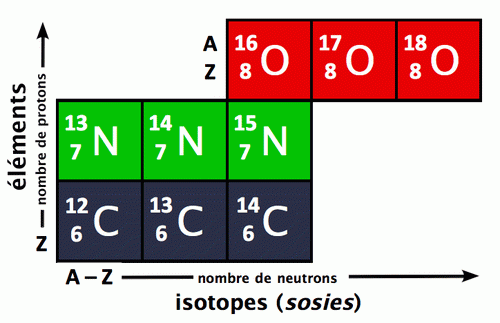
Điều còn lại là tìm hiểu kỹ hơn về cấu trúc của lõi nguyên tử. Năm 1911, khi bắn một chùm tia alpha vào khí đạm, Rutherford chứng tỏ được là lõi của khí Hydrô cũng nằm trong lõi của các đơn chất khác, do đó đây phải là một hạt cơ bản, được đặt tên là proton (nghĩa là đầu tiên), mà điện tích là -1 và khối lượng bằng khoảng 1836 lần khối lượng điện tử (khối lượng của proton sẽ được dùng làm đơn vị khối lượng cho các vi hạt nguyên tử). Về một mặt khác, sau những kết quả khó hiểu từ những thí nghiệm trên một loại tia bị hiểu nhầm là tia phóng xạ gamma (xem một đoạn sau), James Chadwick (giải Nobel vật lý năm 1935) khi bắn tia alpha vào các nguyên tử beryllium, khám phá ra một hạt cơ bản có khối lượng 1 và điện tích 0, đặt tên là neutron. Cho đến ngày nay, hình ảnh nguyên tử quen thuộc với đại chúng vẫn là một mô hình hành tinh đơn giản (hình 2.1) : ba hạt cơ bản là proton, neutron và điện tử ; điện tử quay chung quanh lõi nguyên tử trên những quỹ đạo khác nhau (nói đúng hơn là những tầng quỹ đạo), lõi nguyên tử là một kết hợp của protons và neutrons (hai hạt này vì thế còn được gọi là nucléons) ; Số nguyên tử Z là số proton (bằng số điện tử), khối lượng A của nguyên tử là khối lượng của lõi, tức là do các khối của neutron và proton cộng lại.
Nhưng phải công nhận rằng, mô hình đơn giản này rất giống một sự giản lược quá trớn. Quả là mô hình Rutherford trên thực tế thoả mãn được hầu hết các nhu cầu của hoá học : các liên kết hoá học là do kết hợp điện tử, các con số nguyên tử có thể "giải thích" tính tuần hoàn của bảng Mendeleïev (một cách sắp xếp các đơn chất theo kinh nghiệm, tuỳ thuộc vào những đặc điểm có tính tuần hoàn (xem hình 2.2), khối lượng nguyên tử "giải thích" sự hiện hữu của các chất đồng vị (có cùng số nguyên tử Z, nhưng có khối lượng A khác nhau), v.v.
Nhưng với vật lý học thì mô hình hành tinh không tốt đẹp như thế, nó vừa không đầy đủ, vừa không ổn định. Không ổn định ngay từ quan niệm gốc : theo các quy luật của Maxwell, các điện tích khi chuyển động phải phát ra bức xạ, và như thế các điện tử phải mất đi năng lượng và rơi vào lõi nguyên tử ; ngay ở trong lõi, các proton mang cùng điện tích dương, phải đẩy lẫn nhau, v.v. Không đầy đủ, vì mô hình bỏ qua không giải thích được những hiện tượng như là sự cố kết của lõi, kết cấu bởi một "lực liên kết" bí ẩn và không hề được phát hiện (và chẳng hề không đáng để ý, như ta sẽ thấy trong chương 3) ; và sự phân rã của nó trong hiện tượng phóng xạ – tự nhiên (Becquerel, 1896) hay nhân tạo (vợ chồng Joliot-Curie, 1934) – nói rõ hơn, sự phân rã hay biến đổi một số lõi nguyên tử, kèm theo sự bắn ra các vi hạt và phát sóng (phóng xạ alpha sinh ra hélium, bêta sinh ra các điện tử, gamma phát ra một loại sóng có khả năng xuyên thấu còn cao hơn tia X) có vẻ như vi phạm nguyên lý bảo tồn năng lượng, v.v.
Hình 2.1 :
Bảng tuần hoàn các đơn chất
và vị trí các chất đồng
vị

Hình 2.2 Bảng tuần hoàn các đơn chất
Thực tế cho thấy, công việc giải thích "lực làm rung động những vi hạt trong nguyên tử và giữ cho cái hệ mặt trời tí hon này được ổn định", theo như ước vọng của Max Planck (và chúng ta sẽ thấy ông còn quá ngây thơ), sẽ là công trình chủ yếu của vật lý lý thuyết trong thế kỷ 20, nhưng trước đó phải thực hiện hai cuộc cách mạng ý tưởng đã.
Vào cuối thế kỷ 19, khi làm bản tổng kết tình hình của vật lý lý thuyết năm 1990, Huân tước Kelvin (tên thật là William Thomson, đừng nhầm với J. J. Thomson đã được nói đến) thoải mái chấp nhận rằng "chỉ còn hai đám mây nhỏ trong bầu trời quang đãng" của vật lý học – một là "tai biến cực tím", và một nữa là "tại sao không có gió ête" – nhưng ông không hề nghi ngờ là hai cụm mây nhỏ đó rồi sẽ tan đi. Chỉ vài tháng sau đó, cụm mây đầu tiên nổ ra mưa gió.
Cuộc cách mạng lượng tử
"Tai biến cực tím" là cái tên gợi hình được dùng để gọi sự bất đồng giữa kết luận của lý thuyết và kết quả thực nghiệm trên bức xạ điện từ của "vật đen" – một vật thể hoàn toàn cân bằng nhiệt động so với môi trường chung quanh. Lý thuyết cổ điển chỉ ra rằng bức xạ của vật đen độc lập với mọi chất liệu cấu tạo ra nó, mà chỉ tuỳ thuộc vào nhiệt độ của nó. Vấn đề đặt ra khi ấy là, khi biết nhiệt độ T, mô tả được phổ năng lượng điện từ của vật đen, nói cách khác, tính ra được hàm theo tần số của mật độ năng lượng trong một đơn vị thể tích của vật thể. Các kết quả thực nghiệm vẽ ra một hình chuông bất đối xứng, dạng nhọn hay tù tuỳ theo nhiệt độ (hình 2.3 và 2.4). Đối với các tần số thấp, nhiệt động học cổ điển cho ra những tính toán xấp xỉ khá đúng (định luật Rayleigh-Jeans), nhưng với các tần số cao (tương ứng với bước sóng ngắn), lý thuyết cổ điển tiên đoán một cách phi lý là năng lượng tiến đến vô tận : đó là tai biến cực tím ! Năm 1900, định luật Planck chỉnh đốn được tình trạng khi tính toán đúng năng lượng bức xạ, qua một công thức rất ấn tượng, hội tụ ba hằng số vũ trụ là : vận tốc ánh sáng c, hằng số Boltzmann k, và một hằng số mới, h, dấu ấn đóng trên giấy khai sinh của lý thuyết lượng tử. Lượng tử đến từ danh từ quantum, có nghĩa đại lượng cơ bản. Trong lý luận của Planck, để sử dụng được lý thuyết nhiệt động học thống kê (xem chương 1) ông đặt ra định đề là những trao đổi năng lượng giữa vật đen và các sóng bức xạ điện từ được thực hiện một cách không liên tục, nói chính xác hơn, qua việc trao đổi một số nguyên những quantum tác dụng (tác dụng được lượng tử hoá) mà ở đây ghi ký hiệu là Epsilon. Ý tưởng về sự trao đổi năng lượng một cách gián đoạn này là hoàn toàn cách mạng, vừa ngược lại với trực giác, vừa ngược lại những định kiến của nền vật lý đương đại (điều này có lẽ giải thích vì sao phải đến 1918 Planck mới được trao giải Nobel).
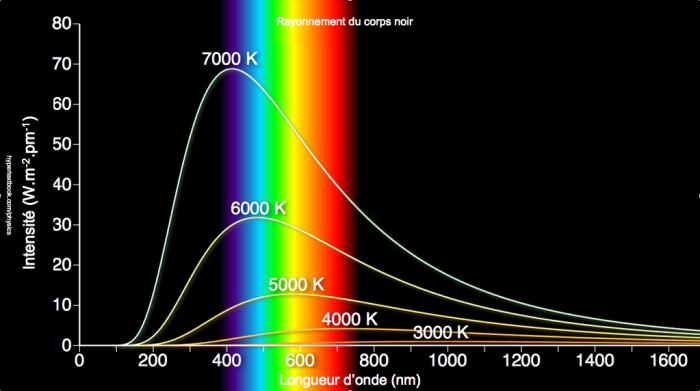
Hình 2.3 :
bức xạ của vật đen : kết quả
thực nghiệm
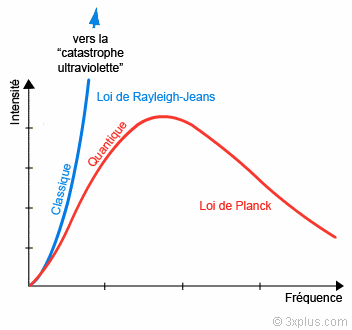
Hình 2.4 :
bức xạ của vật đen : các mô
hình lý thuyết
|
Để tính Epsilon, Planck lượng định entropy của vật đen bằng hai cách khác nhau, một mặt qua việc sử dụng những đặc tính nhiệt động học cổ điển về tương tác giữa sóng điện từ và vật chất, mặt thứ hai là qua sự mô tả thống kê của entropy theo Boltzmann. Để cho hai tiếp cận này có thể tương thích, ông phải chấp nhận là Epsilon tỷ lệ thuận với tần số Nu của bức xạ, do đó ta có Epsilon = h. Nu, trong đó h là hằng số vũ trụ của Planck, h do đó mà có chiều kích là năng lượng nhân với thời gian ( xem [CTS], tr. 107). Với định nghĩa của quantum tác dụng Epsilon này, thống kê Boltzmann cho thấy là mỗi tần số dao động mang theo nó một năng lượng có giá trị trung bình là h.Nu/exp(h.Nu/kT) - 1 ; Nhân năng lượng này với mật độ của mọi tần số có thể có, người ta được kết quả là "mật độ năng lượng Planck", biểu diễn đúng đắn bức xạ vật đen ở nhiệt độ T. |
Kể từ đây người ta sẽ gọi là "lượng tử" tất cả các hiện tượng và các lý thuyết trong đó có tham dự – trực tiếp hay gián tiếp – hằng số vũ trụ Planck. Bạn đọc dù không chuyên chắc hẳn đã cảm nhận được là, đến giai đoạn này, sự "rời rạc hoá" (lượng tử hoá) khái niệm năng lượng là một bước đầu tiên đi tới sự thống nhất điện từ học và cơ học mà từ đầu bài chúng tôi đã nói tới.
Vào "năm thần diệu" 1905, năm mà Einstein công bố thuyết tương đối hẹp và lý thuyết về chuyển động Brown, ông cũng nắm lấy ý tưởng lượng tử để diễn tả hiệu ứng quang điện, nghĩa là sự nảy sinh một dòng điện (tử) khi có bức xạ chiếu vào một vật thể mang đặc tính quang điện này (thí dụ như một chất lỏng trong thí nghiệm của Becquerel năm 1939, với hai điện cực nhúng trong đó) : Hiệu ứng chỉ xẩy ra khi tần số bức xạ cao hơn một ngưỡng nào đó, và khi ấy năng lượng của hạt điện tử bắn ra không phụ thuộc vào cường độ của bức xạ. Nếu chỉ dựa trên tính chất sóng của bức xạ thì không thể giải thích hiện tượng này. Ngược lại, vấn đề sáng rõ ngay khi dùng khái niệm lượng tử : vì năng lượng của bức xạ chỉ được truyền vào chất quang dẫn theo bội số của quantum tác dụng, tỷ lệ với tần số của bức xạ. Ngưỡng tần số của bức xạ chính là ngưỡng năng lượng mà khi truyền đến điện tử trong nguyên tử, được liên hệ với năng lượng liên kết giữa điện tử và nguyên tử. Nếu năng lượng liên kết nhỏ hơn quantum tác dụng của bức xạ thì điện tử bị bắn ra khỏi nguyên tử, và năng lượng của nó không phụ thuộc vào cường độ của bức xạ (xem [CTS] tr.109). Qua diễn tả này, Einstein đã mang trở lại theo cách của ông quan niệm "hạt ánh sáng" của Newton, nhưng ở một đoạn sau chúng ta sẽ thấy là "hạt ánh sáng" này, được thay thế bởi lượng tử ánh sáng tên là photon, là một "vi hạt không có khối lượng", vì nó di chuyển với vận tốc ánh sáng. Einstein sẽ được giải Nobel năm 1921 vì đã giải thích hiệu ứng quang điện (chứ không phải vì lý thuyết tương đối, như hay bị hiểu nhầm).
Năm 1913, theo bước Planck và Einstein, Niels Bohr (giải Nobel 1922) đã lượng tử hoá mô hình nguyên tử bằng cách đặt ra hai nguyên lý :
– Một điện tử chỉ có thể di chuyển trong một vài quỹ đạo ổn định, hoàn toàn tách rời nhau (lượng tử hoá quỹ đạo)
– Điện tử khi di chuyển trong một quỹ đạo ổn định thì không phát ra bức xạ. Nó chỉ phát ra hay hấp thu năng lượng khi thay đổi quỹ đạo (sự chuyển dịch điện tử).
|
Bohr xác định các quỹ đạo qua một tính toán năng lượng dùng cả hai nguồn lý thuyết cổ điển và lượng tử. Ta thử lấy nguyên tử hydrô làm thí dụ, nó chỉ có một điện tử với khối lượng m quay quanh một proton độc nhất trên quỹ đạo bán kính r , với vận tốc v . Các công thức cổ điển, về lực hút tĩnh điện (Coulomb) và về động năng của một điểm quay quanh trung tâm (Newton), đưa đến phương trình mv2 = re2, trong đó, để thuận tiện, ta gọi e là điện tích của điện tử chia cho một hệ số lệ thuộc vào "điện môi" của chân không. Nhưng trong động lực học về một điểm vật chất M di chuyển quanh điểm cố định O, còn xuất hiện mômen xung lượng L, bằng tích vectơ của OM và p, trong đó p = mv là vectơ xung lượng (ở đây ta viết các ký hiệu về vectơ bằng chữ đậm, chiều dài của nó bằng chữ thường, chẳng hạn với vận tốc định hướng bằng vectơ v thì chiều dài của nó là vận tốc vô hướng v). Trong chuyển động vòng tròn khảo sát ở đây, L = mrv. Nguyên lý đầu của Bohr được phát biểu chính xác dưới dạng L = n.ћ, trong đó ћ là hằng số Planck được chuẩn hoá bằng cách chia h cho 2π, vậy mrv = n.ћ , với n là một số nguyên (n = 1, 2, 3,…). Liên kết với nhau hai công thức về vận tốc đã thành lập được như thế, người ta thấy rằng các bán kính và năng lượng điện tử của những quỹ đạo có thể có được sắp đặt theo hai chuỗi như sau : rn = an2, trong đó a = ћ2/me2 là «bán kính Bohr», và En = E1/n2, với E1 = me4/2ћ2 là năng lượng của lớp quỹ đạo thấp nhất. Sự lượng tử hoá các quỹ đạo như vậy là tương ứng với sự lượng tử hoá các tầng năng lượng, và nguyên lý thứ nhì của Bohr được định lượng : các quanta năng lượng trao đổi với điện tử khi nó chuyển dịch có dạng E1(1/n2 – 1/n’ 2), trong đó n và n’ là những số nguyên. |
Sự xác nhận bằng thực nghiệm là tức thì, kết quả đã có sẵn trong phân tích quang phổ của chất khí được làm nóng trong môi trường áp suất thấp : theo công thức của Planck, việc lượng tử hoá các tầng năng lượng nói trên phải được diễn dịch thành việc lượng tử hoá các bước sóng trong bức xạ do điện tử phát ra. Và đó quả nhiên là điều người ta quan sát thấy, ví dụ trong quang phổ của khí hydrô, có đúng những vạch như tính toán theo công thức Bohr (xem hình 2.4). Đương nhiên, mô hình Bohr không giải thích được tất cả, chẳng hạn về một vài bất thường nhỏ trong bảng Mendeleïev, cũng như về cấu trúc mịn của các vạch trong quang phổ khí hydro (được phân trùng thành những vạch rất gần nhau), và còn về thí nghiệm của Stern-Gerlach (trong một từ trường theo chiều thẳng đứng và không đồng đều, một chùm nguyên tử bạc tự chia làm hai)...
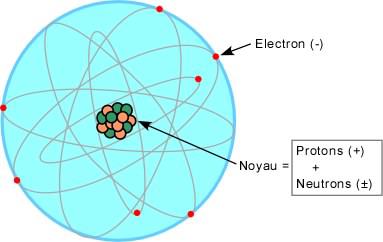
Hình 2.5 :
Mô hình nguyên tử của
Rutherford
Nhưng, mặc dù đây chỉ là những bập bẹ của nền cơ học mới, sự lượng tử hoá các quỹ đạo điện tử đã triệt tiêu được nghịch lý về sự ổn định của chúng. Nhờ vào khái niệm liên quan là ngưỡng năng lượng (mà Einstein đã khai thác), sự lượng tử hoá này còn giải đáp một nghịch lý khác, đó là sự ổn định của nguyên tử, mà vì nó Maxwell từng rơi vào trầm cảm siêu hình khi ông tự vấn về những vi hạt "trong khắp cả vũ trụ, mang theo chúng dấu ấn của một hệ thống đo lường chuẩn nổi bật không kém gì thước đo mét chuẩn trong Viện lưu trữ Paris [và do đó] những phiên bản cùng loại là giống hệt nhau, điều này là một đặc tính thiết yếu của các sản phẩm công nghệ" : thật vậy, một khi mà những nhiễu loạn năng lượng còn nhỏ hơn một ngưỡng nào đó, nguyên tử vẫn là bất khả phân, theo như nguyên nghĩa của nó.
Đồng ý nhưng mà, có người sẽ bảo, còn về sự bất ổn định và sự phân rã của một số lõi nguyên tử thì sao ? Câu trả lời phải được tìm trong cuộc cách mạng khoa học khác kia của thế kỷ 20, lý thuyết tương đối.
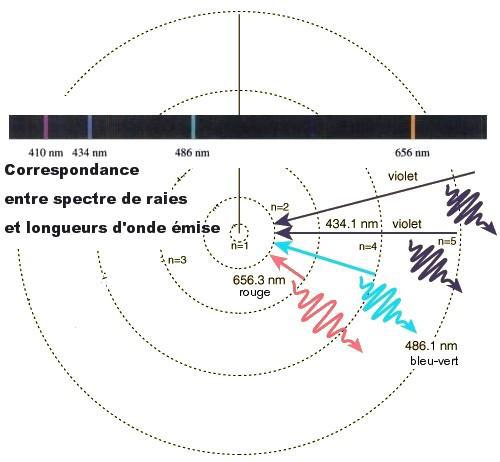
Hình 2.6 : Mô hình nguyên tử của Bohr
Nguyễn Quang
Bản dịch: Hàn Thuỷ
(1) Diễn dịch bị bóp méo (cố ý ?) từ tán thán của nhà vật lý Leo Lederman "cái vi hạt trời đánh này !"
(2) Cuối năm 2011, một nhóm nhà vật lý nghiên cứu trong đề án OPERA công bố quá sớm việc đã phát hiện một loại hạt neutrino di chuyển nhanh hơn ánh sáng. Khi cuối cùng phải công nhận rằng điều ấy chỉ là sai lầm từ một sợi quang dẫn bị hỏng, nhiều thành viên có uy tín của OPERA tự thấy phải từ chức.
(3) Những hộp xám này là các đoạn cũng được viết trong một khung có nền xám
Tài liệu tham khảo:
[B] J. Baggott: La particule de Dieu – A la découverte du boson de Higgs, Dunod, 2013
[CTS] G. Cohen-Tannoudji & M. Spiro : Le boson et le chapeau mexicain – Un nouveau grand récit de l’Univers, Folio Essais, 2013
[GV] C. Grojean & L. Vacavant : A la recherche du boson de Higgs, Librio 2013
Xin lưu ý : ba tài liệu này có trình độ không đồng đều : [GV] vào loại dành cho đại chúng; [B] tập trung trên những khía cạnh lịch sử; còn [CTS] thì có tính chuyên môn khá cao, không phải là sách dành cho người ngoài nghề bắt đầu tìm hiểu.
Các thao tác trên Tài liệu










