Về vật chất - II

- Nguyễn Quang — published 10/12/2013 19:40, cập nhật lần cuối 12/04/2016 22:21

Tất cả những gì bạn vẫn muốn
biết từ lâu về vật chất,
nhưng còn ngại hỏi – Phần-II

Nguyễn Quang

3. Từ Maxwell tới Einstein

Đám mây xám thứ hai trên bầu trời của huân tước Kelvin, chính là thí nghiệm của Michelson-Morley năm 1887 ; nó có khuynh hướng bác bỏ giả thuyết ê-te, và như thế khẳng định sự tồn tại dai dẳng của một mâu thuẫn cơ bản giữa cơ học thuần lý của Newton và lý thuyết điện từ của Maxwell. Cho nên đã đến lúc chúng ta vào tham quan ngôi đền thứ ba của vật lý học thế kỷ 19 này, một tổng hợp sừng sững uy nghi của điện học và từ học, mà còn cả quang học nữa.

Bỏ qua thời tiền sử của bộ môn khoa học này, ta có thể nói là quang học – nhằm tìm hiểu xem ánh sáng di chuyển thế nào ? dưới hình thức nào và theo những quy luật nào ? – bắt đầu phát triển từ đầu thế kỷ 17, với những nghiên cứu của Descartes về màu sắc và sự khúc xạ ; nhưng rồi quan trọng nhất là với sự đối nghịch giữa hai lý thuyết của Newton và Huygens về bản chất của ánh sáng. Trung thành với cách tiếp cận cơ học của mình, Newton quảng bá một quan điểm vi hạt ; dựa trên sự chuyển động của các « hạt sáng », được coi như những điểm vật chất, ông giải thích được một cách tự nhiên những hiện tượng phát tán ánh sáng, giải thích được hiện tượng khúc xạ một cách khó khăn hơn, nhưng bất lực trước các hiện tượng giao thoa và nhiễu xạ. Về phía bên kia, lý thuyết sóng của Huygens đặt giả thuyết là ánh sáng được truyền đi trong một môi trường có tên ê-te, tương tự như những đợt sóng truyền đi trên mặt nước ; để từ đó giải thích dễ dàng những hiện tượng giao thoa, nhưng rồi phải đợi đến đầu thế kỷ 19, với những đóng góp của Young và Fresnel về nhiễu xạ và phân cực ánh sáng, thuyết này mới đánh bại được thuyết Newton.

Sự tổng hợp ba động

Cuối cùng, đợi đến năm 1854, rồi năm 1864, cuộc tổng hợp vĩ đại của Maxwell đã cho phép quy tụ những hiện tượng điện học, từ học và quang học về dưới mái nhà của một khái niệm duy nhất, trường điện từ. Ý tưởng về trường trong vật lý học đã được Faraday đưa ra vào khoảng thập niên 1830, trong những nghiên cứu thực nghiệm của ông về cảm ứng từ. Định nghĩa toán học của một trường, thực rất đơn giản : Xác định một trường trong không gian, hay trong không-thời-gian, tức là xác định ở mỗi điểm của không gian hay của không-thời-gian, một hay nhiều hàm biến thiên liên tục Φ(r) hoặc Φ(r,t) (mà r, hoặc cặp (r,t) là vectơ biểu diễn vị trí của điểm đó). Chẳng hạn như hàm vectơ điện E(r) hay hàm vectơ từ B(r) trong vật lý cổ điển, mà người ta có thể nhìn thấy trong thí nghiệm với mạt sắt, khi chúng được định hướng dọc theo các tuyến lực (xem hình 3.1). Nghiên cứu của Maxwell dựa trên các công trình của những người đi trước như Gauss, Ampère và Faraday, nhưng (theo [CTS]), Einstein và Infeld đã nhấn mạnh rằng ý tưởng về trường điện từ, do Maxwell đem vào trong lý thuyết của ông, là một sự đổi mới quan trọng về khái niệm so với cơ học thuần lý : « Những phương trình của Maxwell mô tả cấu trúc của trường điện từ. Sân khấu của các quy luật này là toàn bộ không gian, chứ không phải như trong các quy luật cơ học, chỉ tính đến các điểm có sự hiện hữu của vật chất và các định lượng của chúng (…) Trường ở đây và bây giờ phụ thuộc vào trường của vùng ngay bên cạnh ở thời điểm ngay trước đây. Và các phương trình cho phép chúng ta dự đoán về những gì sẽ xẩy ra ở một thời điểm trễ hơn hiện nay một chút tại một nơi xa hơn đây một chút, một khi chúng ta biết rõ các hiện tượng tại nơi đây và bây giờ (…) Kết quả của những suy diễn đó hợp thành sóng điện từ. » (Xem hình 3.2). Hiện thực của những làn sóng đó được Hertz minh chứng bằng thực nghiệm năm 1888 (từ đó có tên « sóng Hertz »).

h31

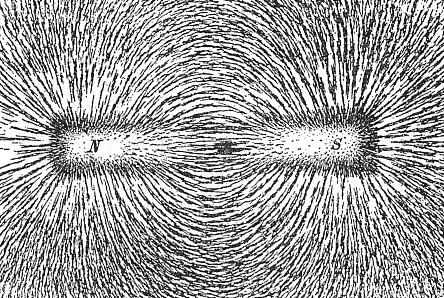
Hình 3.1 Hiển thị một từ trường

h32

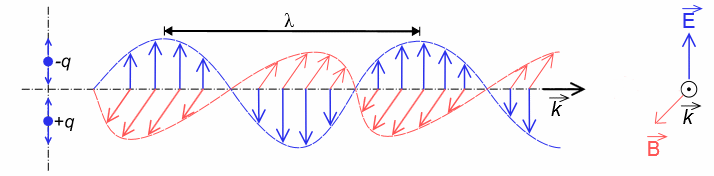
Hình 3.2 Đồ thị của sóng điện từ. λ : bước sóng ;
E: Điện trường dao động ; B : Từ trường dao động

Thực vậy, bốn phương trình đạo hàm riêng cho vectơ mà Maxwell viết ra năm 1854 đã tiên đoán sự hiện hữu của một loại sóng gắn kết với những dao động của từ trường và điện trường, truyền đi trong chân không với một vận tốc mà người ta có thể dễ dàng làm thực nghiệm để đo lường. Sự trùng hợp giữa vận tốc sóng này và vận tốc ánh sáng (trong khoảng sai số của thí nghiệm) khiến cho Maxwell kết luận năm 1864 « rằng ánh sáng và trường điện từ là hai hiện tượng cùng bản chất, và rằng ánh sáng là một biến động của trường điện từ, truyền đi trong không gian theo những quy luật của điện từ học ». Như thế là công trình tổng hợp các loại ba động đã được hoàn thành.

$div\vec{D}=\rho$       (1)
$div\vec{B}=0$    (2)
$\vec{rot}\vec{E}=\,- \frac{\partial \vec{B}}{\partial t}$    (3)
$\vec{rot}\vec{H}=\vec{j}+ \frac{\partial \vec{D}}{\partial t}$ (4)

Nhưng như thế là đồng thời khả năng tổng hợp với cơ học lại rời xa. Hiện chúng ta không bàn đến lưỡng tính sóng-hạt (xem chương 4 dưới đây), mà về một sự không tương thích cơ bản hơn nữa :

Các phương trình Maxwell không bất biến khi thay đổi giữa hai hệ quy chiếu galilê (nghĩa là giữa hai hệ quy chiếu quán tính, chuyển động tương đối với nhau theo đường thẳng với vận tốc cố định), nói cách khác các phương trình này đối nghịch với nguyên lý tương đối galilê, theo đó « các quy luật cơ học là tương đồng trong hai hệ quy chiếu galilê » ; chúng bao hàm ý nghĩa là vận tốc của ánh sáng trong chân không, thường được viết là c, độc lập với các hệ quy chiếu galilê, trong khi mà, theo các quy luật cơ học cổ điển, khi đổi hệ quy chiếu vận tốc ánh sáng phải là kết hợp giữa c và vận tốc tương đối.

Tư tưởng phổ biến đương đại cho rằng các loại sóng không thể truyền đi mà không có một môi trường nền, khi ấy chân không được gán cho ê-te, một môi trường được coi như làm nền cho ánh sáng, ê-te có những đặc tính trái ngược nhau – vừa đủ « chắc » để tải được năng lượng, vừa đủ « lỏng » để không ngăn cản sự di chuyển của các điểm vật chất, nhưng lại cũng phải vừa đủ « có mặt » để cho phép quan sát được các hiệu ứng. Ngầm hiểu rằng mọi chuyển dịch đều phải được coi là chuyển dịch tương đối với một môi trường ê-te cố định (và như vậy đó là một hệ quy chiếu tuyệt đối), người ta thử tìm cách làm hiển lộ, thí dụ như, « gió ê-te » nảy sinh do chuyển động của quả đất. Vậy mà, vào năm 1887, thí nghiệm của Michelson và Morley, có lẽ là « thí nghiệm phủ định » nổi tiếng nhất trong lịch sử khoa học, buộc phải kết luận là không có gió ê-te, bởi vì những cách đo giao thoa cực kỳ chính xác không cho thấy mảy may nào biến đổi của c do chuyển động của quả đất. Nhìn theo cách nào đi nữa, người ta cũng không tránh được mâu thuẫn.

Cuộc cách mạng của thuyết tương đối

Giữa hai năm 1892 và 1904, Hendrik Lorentz mày mò tìm cách biến đổi toạ độ giữ được cho các quy luật Maxwell không đổi. Poincaré đã chỉ ra rằng các biến đổi đó hợp thành một nhóm (theo nghĩa lý thuyết nhóm của toán học, xem chương 6 [trong bài sau] ) được đặt tên là nhóm Lorentz, mà từ đó ông đã suy ra gần như tất cả các phương trình của điều người ta ngày nay gọi là thuyết tương đối hẹp (« về điện động học của điện tử », 1905). Tuy nhiên các sử gia về khoa học thường cho rằng Einstein (« về điện động học của các vật thể đang vận động », 1905) là cha đẻ của thuyết tương đối, vì ông là người đã đem lại giải thích – cách mạng – về vật lý.

Bế tắc của những năm đầu 1900 là do sự đối nghịch giữa các quy luật của Maxwell, bao hàm vận tốc c bất biến, và các quy luật của động học cổ điển, yêu cầu phải kết hợp vận tốc. Vậy mà, thuyết Maxwell có thể hãnh diện vì được nhiều xác nhận qua thực nghiệm, trong khi thuyết cổ điển chỉ dựa trên một định đề duy nhất là sự độc lập với nhau giữa một thời gian tuyệt đối và một không gian tuyệt đối. Với một ý thức táo bạo chẳng kém người đi trước ông là Planck, Einstein đã đứng hẳn về phía Maxwell khi đặt nền tảng cho thuyết của mình trên hai nguyên lý : ông bảo tồn nguyên lý tương đối của Galilê và mở rộng nó ra cho tất cả các hiện tượng vật lý ; và ông thêm vào đó nguyên lý vận tốc bất biến của ánh sáng trong mọi hệ quy chiếu galilê. Với những luận cứ có tính vật lý, ông tìm lại được phép biến đổi Lorentz, từ đó nó trở thành phép biến đổi tự nhiên giữa những hệ quy chiếu galilê.

Cho một chuyển động chỉ thay đổi trục toạ độ x (mọi trường hợp đều có thể quy về trường hợp này), phép biến đổi được viết như dưới đây :

c∆t' = γ(c∆t – β∆x)

∆x' = γ(∆x – βc∆t)

∆y' = ∆y

∆z' = ∆z

và

$$ \Delta t' = \frac{\Delta t - v\Delta x/c^2}{\sqrt{1-v^2/c^2}}$$ $$ \Delta x'= \frac{\Delta x - v\Delta t}{\sqrt{1-v^2/c^2}} $$

∆y' = ∆y

∆z' = ∆z.

Khi đặt $ \beta =\frac{v}{c}$ và $ \gamma = \frac{1}{\sqrt{1-\beta^2}} $

Trong dạng ma trận :

$ \begin{bmatrix} c\Delta t' \\ \Delta x' \\ \Delta y' \\ \Delta z' \end{bmatrix} = \begin{bmatrix} \gamma & - \beta\gamma & 0 & 0\\ - \beta\gamma & \gamma & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} c\Delta t \\ \Delta x \\ \Delta y \\ \Delta z \end{bmatrix} $

Chúng ta thấy, chẳng những hệ phương trình này tiệm cận với động học galilê khi vận tốc không đáng kể so với vận tốc ánh sáng c (còn gọi là vận tốc không tương-đối-tính), mà nó còn đem lại hệ luận là vận tốc c không thể bị vượt qua. Từ điểm khởi đầu là không thể gửi thông tin đi xa một cách tức thì, Einstein táo bạo đặt lại vấn đề tính tuyệt đối của bản thân thời gian. Hệ hình mới trở thành một continum bốn chiều mà Minkowski năm 1908 sẽ đặt tên là không-thời-gian, trong đó đơn giản là tác động của các phép biến đổi Lorentz bảo tồn « khoảng cách vũ trụ » (còn có tên khác là độ dài giả).

Δs² = c²Δt²– Δx² – Δy² – Δz² = c²Δt² – Δl²

Để chuyển đổi từ động học cổ điển sang động học tương-đối-tính, ta cần thay thế các đại lượng vectơ quen thuộc, vận tốc và xung lượng, bằng vectơ vận tốc bốn chiều (trong đó τ là thời gian riêng của hạt vật chất) :

$ \mathbf{u} = \left( c\frac{dt} {d\tau}, \frac{dx} {d\tau}, \frac{dy} {d\tau}, \frac{dz} {d\tau} \right), $

và vectơ xung lượng bốn chiều (trong đó E là năng lượng và m là khối lượng)

P = mu = (E/c, p_x, p_y, p_z) ; với :

$E/c = mc\frac{dt} {d\tau}$; $p_x = m\frac{dx} {d\tau}$ ; $p_y=m\frac{dy} {d\tau}$ ; $p_z=m\frac{dz} {d\tau} $ ,

Bởi vì vectơ bốn chiều này tỷ lệ với vận tốc 4 chiều (có độ dài giả c) theo một hệ số bất biến trong phép biến đổi hệ quy chiếu quán tính, ta có trong mọi hệ quy chiếu :

$(E/c)^2 - (\vec{p}\,)^2 = m^2.c^2 $

Đây là « hệ thức phân tán » nền tảng trong cơ học tương-đối-tính, trong đó ta có thể thấy vế đầu là bất biến trong nhóm Lorentz, và do đó khối lượng m, được tính từ hệ thức m² = (E² – p²c²)/c⁴, có tên khối lượng bất biến, là độc lập với mọi hệ quy chiếu quán tính. Trong trường hợp đặc biệt mà điểm vật chất m là cố định trong một hệ quy chiếu, khối lượng ở trạng thái nghỉ này của nó bằng với khối lượng bất biến, và hệ thức khuyếch tán trở thành đẳng thức E₀ =m.c² mà mọi người đều biết ; điều này có nghĩa, ngay cả trong trạng thái nghỉ, một vật thể vật chất hàm chứa một năng lượng nhất định, có thể là khổng lồ vì trị của c rất lớn. Trong cùng hệ quy chiếu đó, nếu hạt vật chất có khối lượng m lớn hơn không, di chuyển với vận tốc v, năng lượng của nó được tính bằng đẳng thức $$E = \gamma.mc^2 = \frac{mc^2}{\sqrt{1-(v^2/c^2)}},$$(trong đó γ là hệ số tương-đối-tính, và γ.m đôi khi còn được gọi là khối lượng đang di chuyển, nhưng đó là một nguồn gốc của lẫn lộn, cũng như tên gọi khối lượng nghỉ). Một lần nữa ta có thể ghi nhận rằng với vận tốc không-tương-đối, người ta được sự xấp xỉ với những kết quả cổ điển, ở đây là động năng cộng với năng lượng nghỉ. Khi vận tốc v tăng lên và tiến đến gần c, mẫu số của hệ số tương-đối-tính tiến về số không, và do đó với một hạt vật chất có khối lượng khác không, năng lượng E tiến đến vô tận. Nhưng vì không thể có một năng lượng vô tận, điều này có nghĩa đơn giản là không thể tăng vận tốc của một hạt vật chất khi nó tiến gần đến c. Nhìn ngược lại, nếu một vi hạt (chẳng hạn như photon) di chuyển với vận tốc ánh sáng, điều đó có nghĩa khối lượng của nó phải bằng không. Như vậy chúng ta tìm thấy trả lời cho một trong những câu hỏi đặt ra ở đầu bài : vì sao mà một vi hạt có thể có khối lượng bằng không ?

Tới đây không thể không trở về những vấn đề khoa học luận mà các khái niệm khối lượng và lực trong cơ học thuần lý cổ điển đặt ra. Trong tác phẩm « Philosophiae Naturalis Principia Mathematica (Các nguyên lý toán học của triết lý về tự nhiên) », Newton đã cảnh báo là ông dùng ngôn ngữ thường ngày để định nghĩa, theo trực giác, khối lượng của một vật thể là số lượng về thể chất hay vật chất nằm trong vật thể đó. Còn về bản chất của vật chất là gì, thì ông lánh mặt sau công thức lừng lẫy «hypotheses non fingo», « tôi không làm giả thuyết ». Nhưng, trong bốn quy luật cơ bản của ông (mà thực ra là bốn nguyên lý), ông đã cài vào hai định nghĩa mà tiên thiên là khác nhau, về khối lượng : trong quy luật thứ hai, khối lượng quán tính được định nghĩa qua hệ thức nổi tiếng lực = khối lượng * gia tốc, như vậy lực quán tính là cái gì ngăn cản sức đẩy cho vật thể chuyển động ; rồi sau đó, trong quy luật thứ ba, khối lượng hấp dẫn được định nghĩa theo quy luật hấp dẫn phổ quát giữa hai vật thể.

Hẳn rồi, thực nghiệm đã chứng tỏ hai khối lượng này là bằng nhau với sai số dưới 10^-12, và người ta có thể trình bày điều này như một « nguyên lý đồng nhất ». Nhưng điều gây ra thảo luận chính là ý tưởng về lực, được nắm bắt dễ dàng bằng trực giác, nhưng lại rất khó hình dung dưới hình thức khái niệm. Người ta có thể nhận thấy dễ dàng tính chất luẩn quẩn trong những định nghĩa của Newton (vả chăng, các định nghĩa khác trong mọi quyển tự điển cũng đều như thế) và thấy mình, giống như Poincaré, « bị dồn vào sự chấp nhận một định nghĩa, mà cũng chỉ là lời tự thú bất lực, như sau : khối lượng là cái hệ số thêm vào để thuận tiện cho việc tính toán ». Nhưng rõ ràng là, trong một khung cảnh nhất định, các tính toán đó đem lại những kết quả và những tiên đoán đúng, trong nghĩa chúng được thực nghiệm phê chuẩn. Và chúng còn được phê chuẩn bởi những ứng dụng kỹ thuật⁽¹⁾ nữa. Chẳng hạn như, trong khung cảnh tương-đối-tính, những khẳng định thực trái ngược với trực giác, như không gian và thời gian bị nén lại, mà các công thức của Lorentz đã tiên đoán, được người đi đường sử dụng hàng ngày trong hệ thống GPS. Thế thì người ta không thấy có gì bất tiện khi chấp nhận quan điểm thực dụng, được tóm gọn trong khuyến cáo của Dirac (hay có khi là của Feynman, câu chuyện rất có thể do nguỵ tạo) : «Shut up and calculate!» (hãy ngậm miệng lại và tính toán!). Đốn cùng, chẳng ai cần xem hình chụp của nguyên tử (trong chương 1) trước khi tán đồng một lý thuyết nguyên tử mà hàng thập kỷ nay đã cho chúng ta những bằng chứng về hiệu quả (ngay cả quá đáng) của nó : bom A, các trung tâm năng lượng nguyên tử, và những ứng dụng thường nhật của các lý thuyết tương-đối-tính. Còn về thuyết lượng tử, xin xem chương 4 phía sau.

Tính tương đương giữa khối lượng và năng lượng, hiện hình từ những phương trình của Einstein, cho phép trả lời một số câu hỏi mà chúng ta đã tự đặt ra trong chương trước, về nguyên tử và về các vi hạt :

* Độc lập với mọi liên hệ với một hạt vật chất hay về một vật thể vật chất rất nhỏ, danh từ vi hạt từ đây sẽ chỉ một quantum năng lượng, có thể nó hiện ra như năng lượng (và sẽ là một vi-hạt-năng-lượng, hay vi hạt không có khối lượng). Nhưng tính tương đương của Einstein không phải là sự đồng nhất, vì nếu không thì vật chất và năng lượng sẽ chuyển hoá từ dạng này sang dạng kia một cách vô chính phủ, thế mà thực tế không phải như vậy. « Không có gì mất đi, không có gì tự nhiên tự sáng tạo, tất cả là sự đổi thay » Lavoisier đã nói như thế sau Lucrèce. Lý thuyết lượng tử chính là lý thuyết nhằm tìm hiểu những thể thức hoán đổi năng lượng / vật chất.

*Mặc dù không thể giải thích một cách chi tiết về « lực liên kết » bên trong lõi nguyên tử, ít ra tính tương đương của Einstein cũng cho phép ta hiểu những biểu hiện của nó. Chẳng hạn như một vi hạt alpha, lõi của khí hêlium, có khối lượng nhỏ hơn khoảng 1% tổng khối lượng của 2 protons và 2 nơtron hợp thành ra nó. Sự « thiếu khối lượng » không thể giải thích được bằng cơ học cổ điển này đại diện cho năng lượng liên kết, tức khoảng 28 MeV. Còn gây ấn tượng hơn nữa là sự phân hạch (còn gọi là phân rã nguyên tử hay phân rã hạt nhân), xẩy ra khi một lõi nguyên tử nặng hấp thụ một vi hạt khác và lõi phức hợp này bị phân rã thành nhiều mảnh. Trong thí dụ mà một khối lượng M bị phân rã thành hai khối lượng m và m', hệ thức phân tán tương-đối-tính cho thấy dễ dàng là M > m+m', và tính ra được năng lượng thiếu hụt M – (m+m'). Ở tầm con người, việc nhân với hệ số c² cho một năng lượng rất lớn, mà ta không thể lấy năng lượng của những phản ứng hoá học để lượng định. Chẳng hạn như, trong phản ứng phân hạch của nguyên tử urani 235 khi nó hấp thụ một nơtron, năng lượng liên kết được giải phóng ra tương đương với một Mêgawatt-ngày cho mỗi gram urani bị phân hạch. Những nơtron bắn ra khi phân hạch lại có thể được hấp thụ và gây ra một phản ứng dây chuyền : khi phản ứng bùng nổ, đó là bom A, khi được điều tiết, ta có năng lượng của các nhà máy điện nguyên tử. Trong chiều ngược lại, sự tổng hợp hạch nhân, tức là sự kiện hai lõi nguyên tử nhẹ hợp lại thành một lõi nguyên tử nặng hơn (thí dụ một lõi dơteri và một lõi Triti tổng hợp với nhau sẽ cho ra một lõi Heli và một neutron) sản xuất ra một năng lượng còn đáng kể hơn, vẫn do giải phóng năng lượng liên kết : đó là cơ chế hoạt động trong những vì sao... và trong bom H. Nếu được chế ngự, cơ chế tổng hợp hạt nhân sẽ đem lại miễn phí một nguồn năng lượng vô tận.

Qua hai thí dụ trên, chúng ta thấy rõ hơn lợi ích thực tiễn của việc hiểu rõ hơn lực liên kết bên trong lõi nguyên tử, thực ra chính là điều người ta sẽ đặt tên « lực tương tác mạnh » trong lý thuyết trường lượng tử (xem các chuơng 5 và 6). Về ý nghĩa tổng quát trên phương diện khoa học, cuộc cách mạng của Einstein đã xác định một hệ hình mới, bắt buộc mọi lý thuyết về vật chất – cũng có nghĩa mọi lý thuyết lượng tử – phải được thực hiện trong khuôn khổ continum không-thời-gian của thuyết tương đối.

Trường năng động

Đến đây chúng ta sẽ xem xét một minh họa (vẫn không phải là bàn thêm cho vui, nhưng bạn đọc nếu bị bội thực về chuyên môn có thể đọc sau chương 4) về sự « tương đối hoá » của một lý thuyết vật lý cổ điển. Thí dụ nêu ra cũng không phải tình cờ, mà nằm trong ý hướng nhằm tổng hợp cơ học / điện từ học mà con người mãi đi tìm. Xin hãy nhớ lại cuối thế kỷ 19 (xem chương 2), nhờ vào phương pháp thống kê mà cơ học thuần lý đã thành công sáp nhập nhiệt lượng học vào lý thuyết nguyên tử, khi nguyên tử được lý tưởng hoá như một điểm vật chất. Nhưng việc gắn kết với lý thuyết sóng đã hiện ra như là chuyện phản tự nhiên, do bởi lưỡng tính, nếu không muốn nói là sự đối lập, giữa hạt và sóng :

Các đặc tính vĩ mô của hạt và sóng
	Hạt	Sóng
Vị trí, hay sự tương tác	Cục bộ, không gian chiếm hữu có giới hạn	Không có vị trí nhất định, chiếm hữu không gian và thời gian vô hạn
vận động	quỹ đạo liên tục, vận tốc có giá trị nhất định và quan sát được	cùng lúc lan truyền theo mọi hướng (không thể quan sát trực tiếp « momen » ảo của sóng)
tính rời rạc và có thể đếm được	Vật thể là đếm được và chia được thành nhiều vật thể riêng biệt	Vật thể là không đếm được và không chia được thành nhiều vật thể riêng biệt

Sự tổng hợp sẽ chỉ có thể diễn ra vào giữa thế kỷ 20 (xem các chương 4 và 5), nhưng con đường dài này bắt đầu với sự đột trội của khái niệm trường như chúng tôi đã lưu ý, khái niệm này đã lấn lướt khái niệm (thật đáng bàn cãi) về lực. Bằng một cách nào đó, cơ học thuần lý đã tiên liệu sự phát triển ấy khi nhường chỗ dần cho cơ học phân tích của Lagrange (kể từ 1788) và Hamilton (từ 1833), đó là một công trình chuyển đổi dạng toán học của cơ học sang ngôn ngữ trường (trong ý nghĩa đã được xác định ở một đoạn trên), triệt để loại bỏ những khái niệm về điểm vật chất và lực trong việc nghiên cứu một hệ thống đang vận động.

Ta hãy khảo sát một hệ thống S đang vận động, gồm n điểm vật chất M_i, n có thể là vô tận (thí dụ trường hợp chất lỏng). Trong vật lý cổ điển, mỗi điểm có 3 bậc tự do (tương ứng với vị trí trong không gian của nó) và hệ thống có N = 3n bậc tự do. Mỗi điểm M_i còn mang theo những tham số động thí dụ như xung lượng, $\vec{q}_i = m.\vec{v}_i$. Ý tưởng khởi nguồn là đặt ra một không gian trừu tượng gồm N chiều, gọi là không gian cấu hình, rồi xây dựng trong không gian đó một trường (trong nghĩa đã xác định bên trên) mà ta sẽ gọi là trường năng động của hệ thống S, và giả định trường đó có khả năng mô tả tất cả những trạng thái của S cũng như sự biến chuyển của chúng. Trường đầu tiên vào loại này là trường Lagrange, $\mathcal{L}(q_i, \dot{q}_i,t)$ (trong đó $\dot{q}_i = \frac{dq_i}{dt}$ là đạo hàm theo thời gian), dạng thức của hàm Lagrange này thường có thể được suy ra từ những nhận xét về « tính đối xứng » của S. Trong cơ học cổ điển trường Lagrange chính là hiệu số giữa động năng và thế năng. Điều thiết yếu cần ghi nhớ về không gian cấu hình là nó thuần tuý trừu tượng, cũng như các hàm q_i (từ đó được gọi là những « toạ độ tổng quát hoá »), và vì thế cách đặt vấn đề toán học này có tầm áp dụng rất tổng quát, cho phép khảo sát đủ loại hệ thống phức tạp. Những quy luật chi phối sự vận động của S được suy ra từ một nguyên lý biến phân áp dụng trên một hàm tác dụng được định nghĩa như tích phân của hàm Lagrange trong không gian cấu hình. từ đó nguyên lý tác động cực tiểu có thể được phát biểu như sau :

« Trong tất cả những quỹ đạo có thể nối hai điểm trong không gian cấu hình, quỹ đạo di chuyển thực sự của hệ thống là quỹ đạo cho ra một tác dụng cực trị »

Từ nguyên lý này người ta suy ra những phương trình chuyển động của Euler-Lagrange, trong đó bao gồm tất cả các phương trình cơ học thuẩn lý, thành thử ra cơ học Lagrange hiện ra như một sự tổng quát hoá toán học của cơ học thuần lý, trong đó các khác niệm về lực và điểm vật chất đã bị đào thải. Cơ học Hamilton hoàn thiện hình thức toán học của cơ học Lagrange, trong đó các phương trình vi phân bậc hai của Euler-Lagrange được thay thế bằng những phương trình bậc một dễ dàng hơn của Hamilton-Jacobi. Trường năng động mới này gọi là trường Hamilton :

$\mathcal{H} (q_i,p_i,t)=\sum\limits_k^N \dot{q}_kp_k-\mathcal{L}(q_i,\dot{q}_i,t) $

trong đó $ p_i \equiv \frac{\partial \mathcal{L}}{ \partial\dot{q}_i}$ được gọi là momen liên hợp của q_i.

Trong cơ học cổ điển, trường Hamilton chính là toàn thể năng lượng, tổng của động năng và thế năng.

Một lần nữa, điều quan trọng cần ghi nhớ về những định nghĩa nói trên là chúng thuần tuý trừu tượng, nằm trong khung cảnh của những trường tổng quát của không gian cấu hình... Dưới đây chúng ta sẽ đưa ngay những phương pháp này vào ứng dụng cho trường điện từ tương-đối-tính (và sau đó cho các trường lượng tử). Nguyên tắc của phương pháp khai triển cũng đơn giản.

Những trường điện và từ cổ điển là đạo hàm của một trường (vô hướng) điện thế và một trường (vectơ) hiệu thế từ, và trong thuyết tương đối chúng phải được tổng hợp lại trong một trường vectơ thế năng bốn chiều. Để mô tả những tác động trên các vi hạt tích điện di chuyển trong một trường điện từ, người ta tạo một vectơ dòng điện bốn chiều mà các thành phần gồm điện tích và ba thành phần của vectơ mật độ dòng điện, quy luật bảo toàn dòng điện được biểu diễn qua đẳng thức độ phân kỳ bằng không. Sau đó người ta tính tích phân của tác dụng bất biến (qua nhóm Lorentz), gồm ba số hạng : thứ nhất là số hạng biểu diễn động năng của sự lan truyền trường điện từ khi vắng điện tích, thứ hai là động năng của sự lan truyền vi hạt mang điện tích khi vắng trường điện từ, và thứ ba là số hạng của một thế năng liên quan đến tương tác giữa trường điện từ và vật chất. Áp dụng nguyên lý tác dụng cực tiểu, người ta từ đó suy ra những phương trình Maxwell (tương-đối-tính). ([CTS] tr.88).

Tóm lại, với dạng thức toán học Lagrange, ta nắm được một phương pháp luận có hệ thống để viết ra những phương trình mô tả sự vận động của các hệ thống đa dạng, với điều kiện đưa vào một số điều chỉnh và mở rộng thích hợp với mỗi hệ thống (nhưng đấy chính là trọng tâm của từng bài toán). Tuy nhiên, đó chỉ là một dạng thức toán học, không làm cho Einstein thoả mãn ở chỗ được ông nêu ra : « trong mọi lý thuyết cơ bản khác, không thể có việc cùng hiện hữu điểm vật chất, mà sự vận động được chi phối bởi những phương trình vi phân bình thường ; và trường, mà sự vận động được chi phối bởi các phương trình vi phân có đạo hàm riêng » ([CTS] tr.149), do đó mà ông đã kiên trì cố gắng tìm cách suy diễn ra khái niệm điểm vật chất trong một lý thuyết về trường, nhưng không thành công. Cuộc săn tìm này sẽ chỉ được kết thúc với lý thuyết trường lượng tử (đón xem hai chương 5 và 6).

4 - Từ cơ học ba động đến cơ học lượng tử

Sự việc vừa kể đưa ta về một bài báo của Einstein tựa đề « Thuyết điện từ về bức xạ », trong đó ông nhận xét rằng những quanta tác dụng của bức xạ điện từ mang theo nó không những năng lượng mà còn, trong một số trường hợp, một vectơ xung lượng. Đó là trường hợp « hiệu ứng Compton » (1923), trong đó một photon (do tia bức xạ gamma truyền đi) khi va chạm không đàn hồi với một điện tử thì không phải chỉ truyền cho nó năng lượng mà cả xung lượng nữa : photon được khuếch tán sau va chạm này có năng lượng nhỏ hơn, điều thấy được qua bước sóng trở nên dài hơn, nhưng đồng thời các quỹ đạo của điện tử khuếch tán và photon khuếch tán bị phân kỳ so với photon đi tới, theo những góc độ có thể tính được theo cơ học tương-đối-tính. Như thế là có một bước tiến triển trong ý tưởng về lưỡng tính của ánh sáng, nó là sóng, và cũng là hạt. Trong luận án bảo vệ năm 1924, Louis de Broglie đã ký giấy khai sinh cho cơ học ba động khi táo bạo mở rộng lưỡng tính sóng-hạt cho mọi hạt vật chất trong thế giới vi mô. Lý luận của de Broglie vừa sử dụng thuyết lượng tử, vừa sử dụng thuyết tương đối.

Khởi đi từ giả thuyết là hệ thức E = h.υ bao hàm sự hiện hữu của một tần số « riêng » υ liên kết với vi hạt đang được xem xét, và không cần để ý đến hiện tượng rung động mà tần số là υ, ông tìm cách liên hệ bước sóng λ với xung lượng tương-đối-tính của vi hạt. Ta nhớ lại rằng, với các sóng thì tích số λ.υ được gọi là « vận tốc pha », có ký hiệu v_φ. Để tính biến số này, de Broglie định ra một nguyên lý « đồng pha », theo đó « hiện tượng tuần hoàn có chu kỳ υ’ trong hệ quy chiếu riêng của vi hạt luôn luôn đồng pha với một sóng lan truyền theo cùng hướng với vi hạt đang chuyển động » [một loại sóng dẫn-đạo, có thể nói thế]. Trong trường hợp một khối lượng m (ở trạng thái nghỉ), có chuyển động thẳng đều với vận tốc v, áp dụng một cách đơn giản các định nghĩa và phép biến đổi Lorentz, ta có v.v_φ = c² và υ = γ.υ’, trong đó như thường lệ γ là hệ số tương-đối-tính, $1/ \sqrt{1-v^2/c^2}$. Đã biết E = h.υ = γ.mc², người ta suy ra ngay công thức de Broglie, λ.p = h, với p là xung lượng tương-đối-tính.

Bình luận của Einstein : « De Broglie đã vén lên một góc màn ». Năm 1927, thí nghiệm « quyết định » của Davisson và Germer, khi bắn một chùm điện tử chậm vào một tinh thể nickel, đã làm xuất hiện một hình dạng nhiễu xạ (xem hình 4.1 và 4.2), như thế là đã xác nhận được lưỡng tính sóng-hạt, và đem lại giải Nobel cho de Broglie năm 1929. Năm 1931, kính hiển vi điện tử, trong đó các photons được thay thế bằng điện tử, đã đưa cơ học ba động vào thực dụng. Nhưng các lý thuyết gia đã không đợi sự khẳng định này để toàn lực lao vào đặt lại cho cơ học một nền tảng lượng tử. « Các tác phẩm nền tảng của cơ học lượng tử, dạng thức toán học và sự diễn dịch chúng, đã được xây dựng trong những năm 1925 và 1926 bởi một nhóm nhỏ các nhà nghiên cứu xuất sắc ở bốn phương của một châu Âu vừa bị chiến tranh xâu xé ; và họ, chỉ trong vài năm, đã thực hiện một công trình kỳ lạ nhất của trí tuệ con người » (M. Crozon). Đó cũng là một trong những công trình làm cho trí tuệ con người bị rối loạn nhất, nó tách rời khỏi trực giác thường nghiệm xa đến nỗi mà cho đến nay, mặc dù những thành quả chói lọi, nó vẫn gây ra những bàn cãi không cùng về khoa học luận.

h41

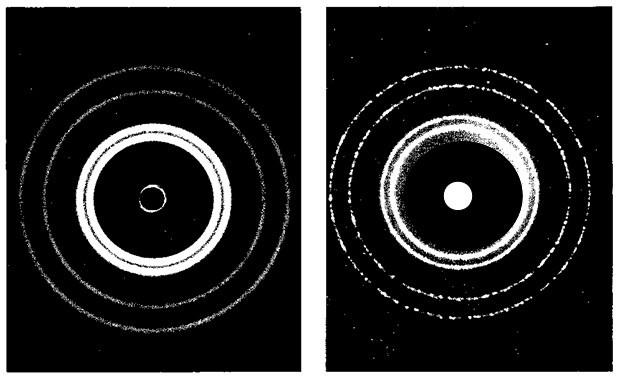
Hình 4.1 Nhiễu xạ của của tia X quang (bên trái), và nhiễu xạ chùm điện tử (bên phải)

h42

Hình 4.2 Nhiễu xạ của chùm điện tử

Cơ học ba động còn chưa trở thành cơ học lượng tử khi Erwin Schrödinger tiến vào triển khai hàm biến thiên theo thời gian của phương trình sóng de Broglie. Ý tưởng để khởi đầu của Schrödinger, hoàn toàn phù hợp với quan điểm lưỡng tính, là nghiên cứu sự tương đồng hình thức giữa quang học và cơ học ; nói chính xác hơn là, giữa nguyên lý biến phân của Fermat trong quang học hình học (ánh sáng truyền đi từ điểm này sang điểm khác trên một con đường mà cục bộ ở mỗi nơi thời gian di chuyển là cực tiểu), và nguyên lý tác dụng cực tiểu trong cơ học phân tích (phương trình Hamilton-Jacobi). Thế rồi, đối đầu với những khó khăn kỹ thuật nghiêm trọng, ông phải chịu hạn chế vấn đề trong khuôn khổ không tương-đối-tính, và năm 1926 Schrödinger đạt tới phương trình đạo hàm riêng tuyến tính ngày nay mang tên ông :

$i\hbar\frac{\partial\Psi(t,\vec{r}\,)}{\partial t}=-\frac{\hbar^2}{2m}\vec{\Delta}^2\Psi(t,\vec{r}\,)+V(t,\vec{r}\,)\Psi(t,\vec{r}\,)$

$\frac{\hat{\vec{\mathbf{P}}\,}^2}{2m}|\Psi(t)\rangle+V(\hat{\vec{\mathbf{r}}},t)| \Psi(t)\rangle=i\hbar\frac{\mathrm{d}}{\mathrm{dt}}|\Psi(t)\rangle $

$ (i\hbar\frac{\partial \mathit{\Psi}}{\partial t}(\mathbf{x},t)= \left( mc^2\alpha_0 - i\hbar c\sum\limits_{j=1}^{3}\alpha_j\frac{\partial{}}{\partial{x_j}}\right)\mathit{\Psi}(\mathbf{x},t)$

Phương trình thứ nhất là phương trình không tương-đối-tính của Schrödinger ; phương trình thứ nhì cùng nội dung, nhưng được viết dưới dạng toán tử thao tác trên những vectơ trạng thái (xem phía sau) ; thứ ba là phương trình tương-đối-tính của Dirac, cũng viết dưới dạng toán tử.

Schrödinger không thể đạt tới dạng phương trình tương-đối-tính vì không sử dụng khái niệm spin (tiếng Anh, có nghĩa là quay như con vụ) của vi hạt. Sau ông, hai phiên bản tương-đối-tính được xây dựng, một do Klein và Gordon năm 1926 cho các vi hạt có spin 0 (như… le boson BEH), và một do Dirac năm 1928 cho các vi hạt có spin ½ (như điện tử). Công trình thứ hai này đưa đến hệ luận – nếu có thể gọi như vậy một khám phá kinh hồn tới mức này – là sự hiện hữu cuả phản vật chất. Việc Anderson năm 1932 đã làm hiển lộ phản-điện-tử (hay positron) trong các bức xạ vũ trụ đã đem lại cho Dirac giải Nobel năm 1933 (chia với Schrödinger). Do Pauli gợi ý, dạng thức lý thuyết được Goudsmit và Uhlenbeck xây dựng năm 1925, spin có thể được mường tượng qua trực giác như momen động riêng của một vi hạt tự xoay vòng. Bậc tự do mới này, cộng vào ba bậc tự do không gian cố hữu, đã hoàn thiện được những khiếm khuyết trong mô hình nguyên tử của Bohr.

Nhưng trực giác phải dừng lại ở đây, bởi vì bản thân Pauli đã chứng minh năm 1924 là một vi hạt có kích cỡ như điện tử, tự quay vòng như con vụ thì phải có một vận tốc tiếp tuyến lớn hơn c ! Trên thực tế, mặc dù spin là một tính chất vật lý chẳng khác gì khối lượng hay điện tích, nó cũng là một tham số lượng tử (còn gọi là số lượng tử, đón xem chương 5) có những giá trị rời rạc ( số nguyên hay số nguyên + ½), không có gì tương đương trong lý thuyết cổ điển, khác hẳn với, thí dụ như, vị trí, xung lượng, năng lượng... Ở đây ta chạm tới tiềm lực của các khái niệm lượng tử, nhưng cũng giáp mặt với sự khó khăn để phổ biến chúng : các khái niệm đã thoát ra khỏi trực giác thường nghiệm, ngôn ngữ toán học thoát ra khỏi cách hiểu bình thường, thế nhưng, các kết quả lại sờ sờ ra đó !

Spin đóng một vai trò quan trọng trong những hiện tượng từ tính và phân cực. việc mà spin của điện tử bằng + ½ hay – ½ (thay vì dấu cộng trừ, người dùng tiếng Anh chuộng nói « up » và « down », có nghĩa « cực Bắc ở trên, hay ở dưới ») giải thích cơ cấu mịn của quang phổ khí hydrô cũng như thí nghiệm Stern-Gerlach. Hơn thế nữa, spin còn có mặt trong những ứng dụng hàng ngày mà người bình thường được thừa hưởng tuy chẳng thể ngờ nó là nguồn gốc : việc thao tác các spin của lõi nguyên tử bằng phương pháp cộng hưởng từ đã đảo lộn công nghệ phổ-học (RMN) và công nghệ hình ảnh y khoa (IRM) ; việc thao tác các dòng spin trong mạch nano đã tạo ra công nghệ « điện tử spin » và cho phép sự bùng nổ của dung lượng bộ nhớ trong thẻ USB, máy nghe MP3, máy điện thoại di động « tài tình » (smartphone), và những thứ vật dụng tinh xảo khác... giải Nobel trao cho Albert Fert năm 2007 là một cách chứng nhận công nghệ điện tử spin.

Cơ học lượng tử có tham vọng cung cấp một khung khái niệm tổng quát cho phép mô tả vận động của các vi hạt ở mức thang nguyên tử. Người ta sẽ phân biệt nó với cơ học ba động một cách võ đoán trên dạng thức lý thuyết của nó, lấy cảm hứng từ cơ học phân tích, và được phát triển vào khoảng trước sau những năm 1930. Cơ học lượng tử trong nghĩa đó được Heisenberg, Dirac, và «trường phái Copenhague» quy tụ chung quanh Bohr phát triển – một dạng thức có tiềm năng phong phú, nhưng, lý thuyết nhằm mô tả thế giới vật chất này lại trừu tượng không gì bằng, có lẽ ngoại trừ thuyết tương đối tổng quát. Đọc tiểu sử Dirac và Heisenberg, người ta có cảm tưởng họ là « những nhà toán học bị đày xuống trần », cho nên không phải tình cờ mà, năm 1930, bản trình bày của Dirac về những nguyên lý của cơ học lượng tử đã dựa trên cơ sở của không gian Hilbert và các toán tử hermite, một lý thuyết rút ra từ bộ môn giải tích hàm. Lại một lần nữa, ta để ý thấy « hiệu quả vô lý của toán học ». Bạn đọc chắc dễ dàng chấp nhận khái niệm trực giác về vectơ, nay xin chấp nhận thêm là không những có thể cộng các vectơ với nhau, mà còn có thể nhân các vectơ với những con số vô hướng có tên là « số phức », được tạo ra từ các số thực bằng cách thêm vào căn số bậc hai của –1 (ghi là i, vậy i² = –1).

Không gian Hilbert là một không gian vectơ có vô tận chiều (với một số vô tận bậc tự do) trong đó được xác định một phép nhân vô hướng (nhân vectơ với vectơ để cho kết quả là một số phức), được định nghĩa như một phép cặp đôi « tuyến tính kiểu một rưỡi », « không thoái hoá »... không cần giải thích ở đây. Một toán tử hermite trong không gian đó là một phép biến đổi các vectơ và tôn trọng các phép toán vectơ, nhưng còn tôn trọng thêm một loại tính đối xứng (mà ở đây cũng không đi vào chi tiết). Diễn tả một cách tổng quát, có nghĩa tránh không quy về bản chất của bất cứ hệ vật lý nào, sáu định đề của cơ học lượng tử được phát biểu như sau :

Cho một hệ thống gồm một số đếm được và không đổi các vi hạt, các trạng thái của nó được biểu diễn bằng những vectơ trong một không gian Hilbert, gọi là vectơ trạng thái, hay hàm sóng, và thường được ghi bằng ký hiệu |x> (đây là quy ước viết có tên « bra-ket » của Dirac)
Những đặc tính có thể quan sát của hệ thống được biểu diễn bằng những toán tử hermite trên không gian Hilbert, đơn giản được gọi là những khả-lượng⁽²⁾. Thí dụ như : toán tử thế năng V, toán tử động năng K, toán tử Hamilton (toán tử tổng năng lượng), H = K + V
Sự đo lường một đại lượng vật lý biểu diễn bằng một khả-lượng A chỉ có thể là giá trị riêng của toán tử đó. Xin nhắc lại là một vectơ riêng |x> của A liên kết với một giá trị riêng a phải thoả mãn đẳng thức A.|x> = a.|x>. Những giá trị riêng của một toán tử hermite luôn luôn là số thực.
Mọi toán tử hermite H đều có một hệ đầy đủ các vectơ riêng e_n sao cho mỗi vectơ |x> của H chỉ có thể bằng một tổng vô hạn và hội tụ của một chuỗi số hạng a_n.|e_n>. Nếu tổng đó biểu diễn vectơ trạng thái |x> (được chuẩn hoá) ngay trước khi đo lường, thì xác suất để đo lường cho kết quả a_n bằng |a_n|², bình phương của môđun của a_n. Tiên đề có tính xác suất này thừa hưởng từ Max Born (giải Nobel 1954)
Ngay sau khi đo lường, vectơ trạng thái trở thành một vectơ riêng tương ứng với giá trị riêng kết quả của phép đo (hiện tượng « giảm-sóng » theo tiếng Pháp, hay « sụp-sóng » theo tiếng Anh)
Trạng thái của mọi hệ thống lượng tử không-tương-đối-tính là một nghiệm của phương trình Schrödinger theo thời gian ; nói cách khác, trường Hamilton khi ấy chi phối vận động theo thời gian của hệ thống.

Niels Bohr có thói quen nói : « người nào không bị choáng trước lý thuyết lượng tử thì là người không hiểu nó ». Thực thế , phản ứng đầu tiên của người ngoại đạo trước 6 tiên đề trên có thể tóm tắt bằng lời tán thán : « thật quái-quái-đản-đản ! ». Người trong nghề thì chắc là có khúc mắc với chính tiên đề có tính xác suất của Max Born. Không đi vào các bàn cãi khoa học luận, chúng ta hãy bằng lòng với việc xem xét kỹ càng một vài hệ luận nổi tiếng của tiên đề 4 :

Nguyên lý bất định của Heisenberg

Định đề 1 xác lập một biểu thức có tính tiên đề về lưỡng tính hạt-sóng ; vì lẽ một sự vật lượng tử có một độ rộng (trong không gian) và có một độ lâu (trong thời gian), biểu thức này không mô tả sự vật bằng một tập hợp những giá trị vô hướng (các toạ độ của vị trí và vận tốc), mà bằng một hàm sóng mô tả sự phân phối của nó trong không gian và thời gian (xem hình 4.3). Nhưng, theo trực giác thì một vi hạt « hoặc ở chỗ này, hoặc ở chỗ kia », trong khi một sóng thì « ở đâu cũng có nó », và công thức của de Broglie kết nói xung lượng với tần số (xem bên trên) đã mang theo mầm mống của một nguyên lý bất định rồi : thí dụ như, nếu biết tần số của sự vật lượng tử thì chỉ biết xung lượng của nó, tức là tích của khối lượng và vận tốc, chứ không biết được cả khối lượng lẫn vận tốc.

Trong dạng thức toán học lượng tử, Heisenberg (giải Nobel 1932) giải thích sự bất định này bằng tính chất « bất giao hoán » của các (toán tử dùng biểu diễn) khả lượng. Thật thế, theo chính định nghĩa của chúng, tích của hai toán tử không nhất thiết phải giao hoán, có nghĩa A.B có thể khác B.A ; hiệu số của chúng, được đặt tên là « (cái-)giao-hoán », viết [A, B], lượng định mức độ không đủ giao hoán. Với những khả-lượng vị trí $\hat{x}$ và xung lượng $\hat{p}$, phương trình Schrödinger có hệ quả là giao-hoán [$\hat{x}$, $\hat{p}$] bằng iħ, trong đó ħ là hằng số Planck đã tiểu chuẩn hoá. Định đề 4 như vậy bao hàm ý tưởng là người ta không thể cùng một lúc lượng định một cách chính xác vị trí và xung lượng, hay nói rõ hơn là tích của độ lêch chuẩn của hai đo lường đó phải lớn hơn hay bằng ħ/2. Một sự mất chính xác tương tự tác động vào cặp năng lượng - thời gian, tích của độ lêch chuẩn phải lớn hơn hay bằng ħ. Vào năm 1927, Heisenberg phát biểu nguyên lý bất định tổng quát (thực ra đây là một định lý, chứng minh từ các tiên đề lượng tử), qua hình thức toán tử dưới dạng sau :

$\Delta A \cdot \Delta B \geq \frac{1} {2} | \langle [ \hat{A},\hat{B}] \rangle_\gamma |$

trong đó A và B là hai khả lượng, $\hat{A}$ và $\hat{B}$ là các toán tử tương ứng,

$\langle\rangle_\gamma$ là trị trung bình của trạng thái $|\gamma\rangle$

Δ X là độ lệch chuẩn của X : $ \sqrt{\langle \hat{X}^2\rangle_\gamma-\langle \hat{X} \rangle^2_\gamma } $

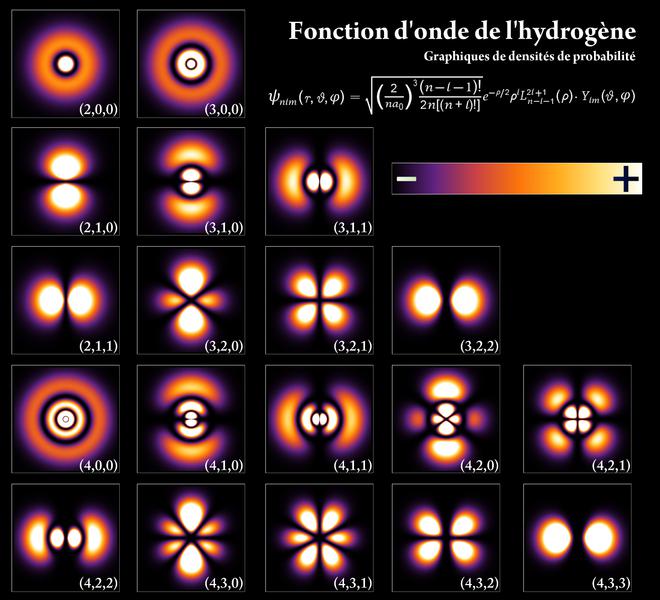
Hình 4.3 Hàm sóng của khí hydrô cùng với mật độ xác suất

Trên quan điểm vật lý, bất đẳng thức trên đây có nghĩa là, do quantum tác dụng của Planck, hễ tăng độ chính xác trong việc đo lường một khả lượng thì lại mất độ chính xác của khả lượng kia. Điều quan trọng cần nhấn mạnh là nguyên lý Heisenberg không nói gì về bản thân sự đo lường nào (chẳng hạn sự tuỳ thuộc vào công cụ đo lường), mà về hiện tượng cơ bản là không thể cùng xác định chúng. Chính vì vậy mà nên nói về nguyên lý bất định, hơn là « nguyên lý mất chính xác ». Dù sao đi nữa, giữa tất định thuyết và nguyên lý bất định, cuộc cãi vã khoa học luận đang nhức nhối hoành hành. Người ta nghe nhiều về câu nói của Einstein « Thượng đế không chơi trò súc xắc », nhưng có lẽ ít người biết câu trả lời của Bohr : « Einstein, ông là ai mà dám bảo Thượng đế nên hay không nên làm gì ? »

Con mèo của Schrödinger

Hai vectơ có thể cộng với nhau, do đó tiên đề 1 và tuyến tính của phương trình Schrödinger trong tiên đề 4 cho phép hai trạng thái bất kỳ được « song trùng » theo cách nói của các nhà vật lý. Nhưng « nguyên lý song trùng » này, khi được ghép với các nguyên lý lượng tử khác về đo lường (tiên đề 2 và 4), sản sinh ra những nghịch lý khi người ta làm song trùng hai trạng thái mâu thuẫn với nhau. Một trạng thái song trùng có thể vui vẻ minh hoạ nghịch lý này được viết như sau :

$(1/ \sqrt{2}).(|s\hat{o}'ng\rangle + |ch\hat{e}'t\rangle)$

(trong đó trị vô hướng ở đầu biểu thức chỉ vai trò chuẩn hoá các vectơ sao cho các xác suất đều nhỏ hơn 1). Cụ thể hơn, Schrödinger đã tưởng tượng ra một thí nghiệm « ở trong đầu », được thực hiện bằng cách nhốt một con mèo trong một cái hộp, cùng với một thiết bị (bình khí độc xyanua, theo Schrödinger, thùng thuốc súng, theo Einstein) nhằm giết chết con mèo ngay khi nó phát hiện một nguyên tử của một chất phóng xạ tự phân rã (xem hình 4.4). Giả thử trung bình sau một phút thì xác xuất nguyên tử tự phân rã là một trên hai, vậy ở thời điểm đó thì con mèo còn sống hay đã chết ? Theo những nguyên lý về đo lường của cơ học lượng tử, một khi chưa được quan sát thì nguyên tử ở trong trạng thái song trùng, có nghĩa, bằng cách nào đó, nó vừa còn nguyên vẹn vừa đã phân rã, và do đó con mèo cũng như thế, vừa sống vừa chết cho đến khi cái hộp được mở ra và kích hoạt (tiên đề 2) sự chọn lựa giữa một trong hai trạng thái. Tóm lại, không phải là không thể trả lời câu hỏi nếu không mở hộp ra xem, nhưng chính là câu trả lời không có trong hộp trước khi người ta mở nó ra !!!.

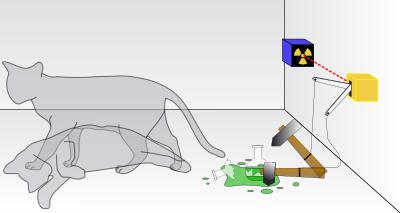
Hình 4.4 Con mèo của Schrödinger

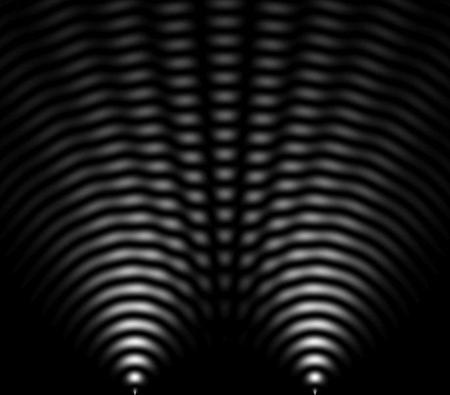
Thực ra, một thí nghiệm tương đương với thí nghiệm giả tưởng có « con mèo quỷ nhập tràng » của Schrödinger có thể được thực hiện trong thực tế, đó là thí nghiệm hai khe của Young. Năm 1801 đây đã là một thí nghiệm « quyết định », làm cho cán cân nghiêng về phía chấp nhận bản chất sóng của ánh sáng (xem chương 3) : khi dùng một nguồn sáng độc nhất chiếu vào một màn che có rạch hai khe hở hẹp, người ta cho thấy hai nguồn sáng xuyên qua màn che và giao thoa với nhau, sự giao thoa hiện lên một màn ảnh thành ra những vạch sáng tối đan xen (xem hình 4.5). Làm thí nghiệm kiểu ấy với những chùm vi hạt, người ta cũng tạo ra được những hình giao thoa, trong khi tưởng rằng chúng phải tụ tập một cách đơn giản thành một mảng trên màn hình sau hai khe. Còn lạ hơn nữa, nếu người ta không bắn cả chùm hạt mà bắn từng hạt một (hạt photon hay điện tử), như trình độ kỹ thuật hiện nay cho phép, sau rất nhiều lần vẫn hiện ra các vạch giao thoa như trong thí nghiệm của Young. Diễn tả của cơ học lượng tử là, cũng như con mèo của Schrödinger, vi hạt ở trong một trạng thái song trùng, « đã qua cả hai khe cùng một lúc ».

Hiệu ứng đường hầm, được sử dụng trong «kính hiển vi dùng hiệu ứng trường / đường hầm» (xem hình 1.1 và 1.2 trong chương 1) cũng thuộc cùng một hiện tượng nghịch lý. Hiệu ứng này là hiện tượng một sự vật lượng tử có thể vượt qua một hàng rào thế năng ngay cả khi năng lượng của nó thấp hơn năng lượng tối thiểu cần đến. Thực vậy, khi gặp hàng rào thế năng thì hàm sóng trở nên yếu đi theo hàm mũ, nhưng cũng không triệt tiêu hoàn toàn (đó là hiện tượng «sóng suy biến» trong điện từ học), thành ra có một xác suất, nhỏ nhưng không bằng không, để vi hạt xuất hiện bên kia hàng rào.

44b

Hình 4.5 Thí nghiệm hai khe của Young

Các vi hạt đi qua hai khe từng hạt một vẫn cho thấy các vạch giao thoa, y hệt như khi thí nghiệm với ánh sáng.

Fermion đối lập với Boson

Mãi tới đây chúng ta mới xây dựng đủ cơ sở để đưa ra định nghĩa cho một boson. Nguồn gốc của cách gọi này là tên nhà vật lý Ấn Độ Satyendranath Bose, người đã cùng Einstein phát triển trong những năm 1920 một phép thống kê lượng tử, để sử dụng trên các photon. Thời đó các nhà vật lý nhận ra rằng phép thống kê cổ điển theo Boltzmann không áp dụng được một cách thuần nhất cho mọi vi hạt, điều này gây khó khăn lớn cho việc phân tích các cấu hình để tính toán entrôpi. Các phép thống kê lượng tử thay thế cho thống kê Boltzmann có liên quan tới hiện tượng không-thể-phân-biệt các hạt đồng nhất theo nguyên lý lượng tử ([CTS] tr.176).

Hãy coi hai vi hạt đồng nhất 1 và 2, có thể ở trong các trạng thái lượng tử a và b, ta ghi bằng ký hiệu |ψ₁> và |ψ₂> hai cấu hình sau : {1 ở a, 2 ở b}, {1 ở b, 2 ở a}. Nhưng vì |ψ₁> và |ψ₂> là không-thể-phân-biệt, định đề 4 bao hàm hệ luận là biên độ xác suất của chúng là hai số phức có môđun bằng nhau ; nghĩa là tích q của hai biên độ đó có môđun bằng 1 ; việc hoán đổi hai vi hạt cho ta thấy q² = 1, vậy q chỉ có một trong hai trị : +1 và -1.

Nếu q = + 1, ta gọi loại vi hạt đó là những bosons (thí dụ các photons) ; nếu q = -1, chúng là những fermions (thí dụ :các điện tử). Người ta chứng minh được bằng toán học rằng spin của các fermions có trị là số nguyên rưỡi, và spin của các bosons có trị là số nguyên (định lý cơ bản liên kết spin và phép thống kê vi hạt). Để nói cho có màu mè, các vi hạt tụ tập thành hai băng đảng, băng đảng theo « cá nhân chủ nghĩa » sẽ ngăn chận chúng ta không cho đi qua, và băng đảng theo « bầy đàn chủ nghĩa » sẽ làm loá mắt chúng ta vì ánh sáng chói lọi. Nói một cách khoa học hơn, những fermions tuân theo phép thống kê có tên «thống kê Fermi-Dirac»; vì q = -1 nên nếu a = b ta thấy ngay là |ψ₁> = 0, nói cách khác, không thể có (hiểu một cách xác xuất) hiện tượng hai fermions đồng nhất cùng trạng thái lượng tử và ở cùng một vị trí ; đặc biệt, điều này giải thích là không thể xâm nhập vào bên trong vật chất, vì proton, nơtron và điện tử đều là những fermions. Về phần chúng, các bosons tuân theo « thống kê Bose-Einstein » : chúng có khuynh hướng kết tập trong những trạng thái lượng tử có năng lượng thấp nhất, nơi các biên độ xác xuất có khuynh hướng cộng lại với nhau ; đó là sự « ngưng tụ Bose Einstein », chính ngưng tụ này giải thích tại sao có hiện tượng « kích phát đồng thời » của các photons (mà Einstein nói đến trong bài báo đã dẫn ở ngay đầu chương này), ở nguồn gốc của hiệu ứng laser.

Cái « hiệu quả vô lý của toán học » của những nguyên lý lượng tử đặt ra cũng vẫn những câu hỏi khoa học luận mà chúng tôi đã gợi ra trong chương 3 về những lý thuyết khác. Thái độ của đa số nói chung vẫn là « sự thực dụng » của trường phái Copenhague, mà Stephen Hawking, trong những ngày vui vẻ, tóm tắt như sau : « Tôi không đòi hỏi một lý thuyết phải phản ảnh hiện thực, vì tôi chẳng biết hiện thực là gì. Đó không phải là thứ người ta có thể thử bằng giấy nghiệm pH [loại giấy có phản ứng đổi màu tuỳ theo độ pH của chất lỏng được thử nghiệm]. Điều quan trọng duy nhất với tôi là lý thuyết tiên đoán đúng đắn kết quả của thí nghiệm ». Còn khi mất vui, ông nói : « Hễ thấy con mèo của Schrödinger là tôi rút súng ra liền ».